Example 3

Detailed description

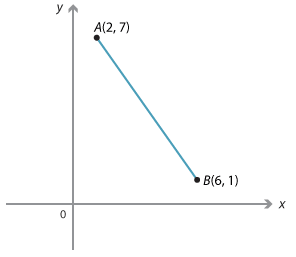
Given the points A(2, 7) and B(6, 1):

\begin{align}\text{gradient of interval}\ AB &= \dfrac{rise}{run} = \dfrac{1 − 7}{6 − 2} = \dfrac{−6}{4} = −\dfrac{3}{2}\\ \\ \text{or}\\ \\ \text{gradient of interval}\ BA &= \dfrac{rise}{run} = \dfrac{7 − 1}{2 − 6} = \dfrac{6}{−4} = −\dfrac{3}{2}\end{align}

Notice that in this case as we move from A to B the y-value decreases as the x-value increases. The gradient is negative. Similarly, the gradient of \(BA = −\dfrac{3}{2}\) which is the same as the gradient of AB.

Detailed description

In general:

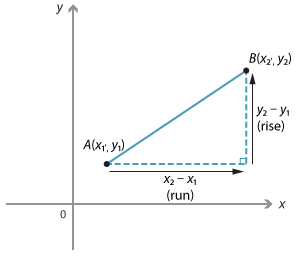
\begin{align}\text{Gradient of line interval}\ AB &= \dfrac{rise}{run}\\ m &= \dfrac{y_2 − y_1}{x_2 − x_1}\\ &= \dfrac{y_1 − y_2}{x_1 − x_2}\end{align}

Special cases

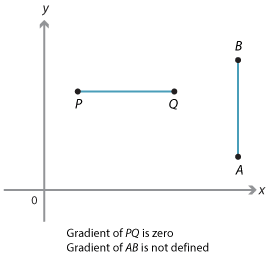
If the interval is vertical, the run is zero and the gradient of the interval is not 
defined. This is shown by interval AB.

If the interval is horizontal, the rise is zero as shown by interval PQ. The gradient of the interval is zero.

Detailed description