Content description

Describe translations, reflections in an axis, and rotations of multiples of 90 ° on the Cartesian plane using coordinates. Identify line and rotational symmetries (ACMMG181)

Source: Australian Curriculum, Assessment and Reporting Authority (ACARA)

There is a separate resource for line and rotational symmetry

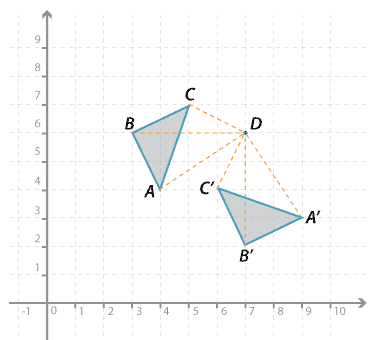
Rotations of multiples of 90° about a point

Detailed description

In the figure above, \(\triangle ABC\) is rotated 90 ° in an clockwise direction about point \(D\) to the image \( \triangle A^\prime B^\prime C^\prime\).

The point \(A\) in the diagram above is rotated 90 ° in a clockwise direction about point \(D\). Note that \(AD = A^\prime D\) and \(\angle AD A^\prime = 90 ^\circ \).

Using coordinates we can describe the rotation of the vertices:

\(A(4, 4) \rightarrow A^\prime (9, 3); B(3, 6) \rightarrow B^\prime (7, 2); C(5, 7) \rightarrow C^\prime (6, 4)\).