Content description
Describe translations, reflections in an axis, and rotations of multiples of 90 ° on the Cartesian plane using coordinates. Identify line and rotational symmetries (ACMMG181)
Source: Australian Curriculum, Assessment and Reporting Authority (ACARA)
Reflections using coordinates
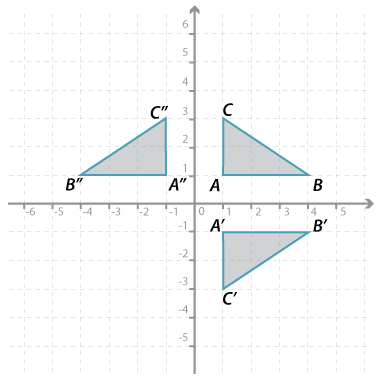
A reflection is a transformation that 'flips' a figure about a line. This line is called the axis of reflection.
In the figure above, \(\triangle ABC\) is reflected in the \(x\)-axis to the image \( \triangle A^\prime B^\prime C^\prime\). The axis of reflection is the \(x\)-axis.
In the same figure, \(\triangle ABC\) is reflected in the \(y\)-axis to the image \( \triangle A^{\prime\prime} B^{\prime\prime} C^{\prime\prime}\). The axis of reflection is the \(y\)-axis.
  |
This publication is funded by the Australian Government Department of Education, Employment and Workplace Relations |
Terms of use  |
