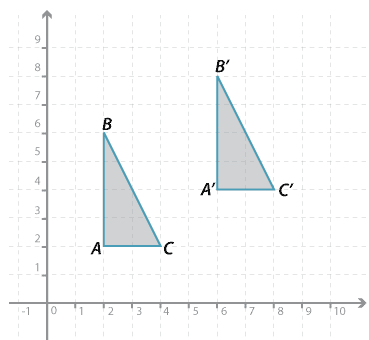![]()
Translations of the Cartesian plane using coordinates
When a figure is shifted in the plane without being turned it is called a translation. To describe a translation it is enough to say how far left or right and how far up or down the figure has moved.
The \(\triangle ABC\) in the diagram has been translated to a new position on the Cartesian plane, and the new triangle has been labelled \(\triangle A^\prime B^\prime C^\prime\).
You can see that it has shifted 4 units right and 2 units up. The point \(A\) has moved to \(A^\prime\) and \(B\) to \(B^\prime\) and \(C\) to \(C^\prime\).
The image of a point is always written with a dash attached. Thus the image of A is written \(A^\prime\) (read '\(A\) prime' or '\(A\) dash'). The image of \(\triangle ABC\) is written \(\triangle A^\prime B^\prime C^\prime\).
The translation has not changed the side lengths or the angles of the triangle. We see:
\(A(2, 2) \rightarrow A^\prime (6, 4); B(2, 6) \rightarrow B^\prime (6, 8); C(4, 2) \rightarrow C^\prime (8, 4)\).
In general, \(P(x, y) \rightarrow P^\prime (x + 4, y + 2)\).