![]()
Alternate angles
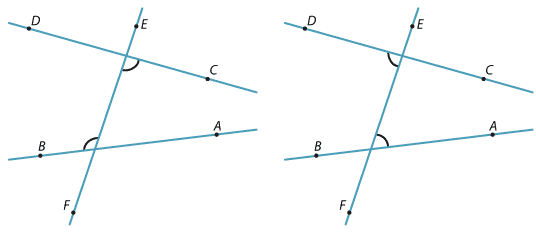
In each diagram below, the two marked angles are called alternate angles because they are on alternate sides of the transversal EF. The two angles must be between the two lines.
Alternate angles and parallel lines
When the lines AB and CD are parallel (as in the diagram below), the alternate angles \(\angle\)BHF and \(\angle\)CGE are equal.
This can be proven using the previous result that showed that corresponding angles are equal.
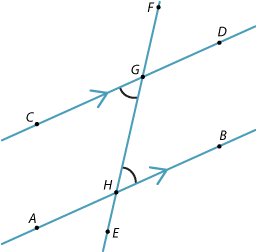
\(\angle\)BHF = \(\angle\)DGF (corresponding AB || CD)
\(\angle\)DGF = \(\angle\)CGE (vertically opposite angles at G)
Hence \(\angle\)BHF =\(\angle\)CGE.
Example 2
Find θ in the diagram.
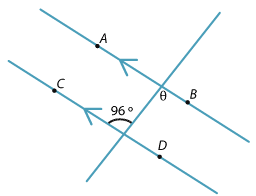
Solution
θ = 96° (alternate angles AB || CD)




