Content description

Investigate and use square roots of perfect square numbers (ACMNA150)

Elaborations

• investigating square numbers such as 25 and 36 and developing square-root notation
• investigating between which two whole numbers a square root lies

Source: Australian Curriculum, Assessment and Reporting Authority (ACARA)

Squares

The square of a number is the number multiplied by itself. For example, four squared, 4², is 4 × 4 = 16.

This can be shown as a diagram.

A square of side length 4 cm has an area of 4 cm × 4 cm = 16 cm².

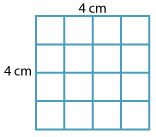
The square root of a number is the number that when multiplied by itself gives the original number.

To illustrate:

6 × 6 = 36, so six is the square root of 36. We write \(\sqrt{36}=6\).

11 × 11 = 121, so 11 is the square root of 121. We write \(\sqrt{121}=11\).

Geometrically, the square root of a number is the side length of a square whose area is that number.