![]()
Content description
Multiply and divide fractions and decimals using efficient written strategies and digital technologies (ACMNA154)
Elaboration
- investigating multiplication of fractions and decimals, using strategies including patterning and multiplication as repeated addition, with both concrete materials and digital technologies, and identifying the processes for division as the inverse of multiplication
Source: Australian Curriculum, Assessment and Reporting Authority (ACARA)
Dividing by a whole number
We have seen how to divide a whole number by a whole number.
For example, \(7÷3=\dfrac{7}{3}=2\dfrac{1}{3}\).
Thus dividing by 3 gives the same answer as finding \(7×\dfrac{1}{3}=\dfrac{7}{3}\).
In general, for whole numbers m and n, dividing m by n is the same as multiplying m by \(\dfrac{1}{n}\).
\(m\div n=m\times\dfrac{1}{n}\)
The fraction \(\dfrac{1}{n}\) is called the reciprocal of n.
Dividing a fraction by a whole number
This same idea can be used when dividing a fraction by a whole number.
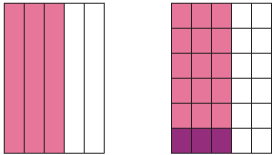
For example, \(\dfrac{3}{5}\div6\) means that we take \(\dfrac{3}{5}\) and divide it into 6 equal parts.
The first diagram shows \(\dfrac{3}{5}\) and the second diagram shows this area divided into six equal parts. The dark shaded area represents \(\dfrac{3}{5}\div6\) and \(\dfrac{3}{30}\).
We note that \(\dfrac{3}{5}\times\dfrac{1}{6}=\dfrac{3}{30}\), so the rule for multiplying by the reciprocal also holds.