Dividing by a whole number

We have seen how to divide a whole number by a whole number.

For example, \(7÷3=\dfrac{7}{3}=2\dfrac{1}{3}\).

Thus dividing by 3 gives the same answer as finding \(7×\dfrac{1}{3}=\dfrac{7}{3}\).

In general, for whole numbers m and n, dividing m by n is the same as multiplying m by \(\dfrac{1}{n}\).

\(m\div n=m\times\dfrac{1}{n}\)

The fraction \(\dfrac{1}{n}\) is called the reciprocal of n.

Dividing a fraction by a whole number

This same idea can be used when dividing a fraction by a whole number.

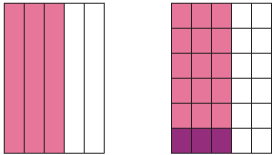
For example, \(\dfrac{3}{5}\div6\) means that we take \(\dfrac{3}{5}\) and divide it into 6 equal parts.

Detailed description

The first diagram shows \(\dfrac{3}{5}\) and the second diagram shows this area divided into six equal parts. The dark shaded area represents \(\dfrac{3}{5}\div6\) and \(\dfrac{3}{30}\).

We note that \(\dfrac{3}{5}\times\dfrac{1}{6}=\dfrac{3}{30}\), so the rule for multiplying by the reciprocal also holds.