![]()
Multiplying fractions
How do we multiply two fractions, such as \(\dfrac{2}{3}×\dfrac{3}{4}\)?
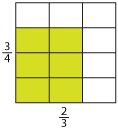
We can look at an area model. Take a square of side length 1 and divide it into rectangles by drawing vertical and horizontal lines as shown below.
We divide the height into quarters and the width into thirds. Each rectangle has an area of \(\dfrac{1}{12}\). If we now shade the region with side lengths \(\dfrac{2}{3}\) and \(\dfrac{3}{4}\), we can see that we have an area of \(\dfrac{6}{12}\). So the area of the shaded region is the product of its sides \(\dfrac{2}{3}×\dfrac{3}{4}\). This is also equal to 6 lots of \(\dfrac{1}{12}\).
We conclude that \(\dfrac{2}{3}×\dfrac{3}{4}=\dfrac{6}{12}=\dfrac{1}{2}\). So we can see that the rule for multiplying two fractions is:
This can be written as
Simplify if possible.
As before, when we say \(\dfrac{2}{3}\) of \(\dfrac{3}{4}\), we mean \(\dfrac{2}{3}×\dfrac{3}{4}\) .
Example 3
- \(\dfrac{3}{4}×\dfrac{10}{7}=\dfrac{3×10}{4×7}\)
- \(\dfrac{1}{6}\ \text{of}\ \dfrac{5}{2}\)
Solution
- \begin{align}\dfrac{3}{4}×\dfrac{10}{7}&=\dfrac{3×10}{4×7}\\\\ &=\dfrac{30}{28}\\\\ &=\dfrac{15}{14}\\\\ &=1\dfrac{1}{14}\end{align}
- \begin{align}\dfrac{1}{6}\ \text{of}\ \dfrac{5}{2}&=\dfrac{1×5}{6×2}\\\\ &=\dfrac{5}{12}\end{align}
Cancelling
Again, we can streamline the process by cancelling before multiplying.
Example 4
Evaluate \(\dfrac{2}{3}\ \text{of}\ \dfrac{3}{4}.\)
Solution
\begin{align}\dfrac{2}{3}×\dfrac{3}{4}&=\dfrac{2^1\hspace{-6mm}\color{darkred}{\setminus}}{3\hspace{-4mm}\color{darkred}{\setminus}}×\dfrac{3\hspace{-4mm}\color{darkred}{\setminus}}{4^2\hspace{-6mm}\color{darkred}{\setminus}}\\\\ &=\dfrac{1}{2}\end{align}Example 5
\(\dfrac{8}{9}×\dfrac{5}{18}×\dfrac{9}{10}\)
Solution
\begin{align}\dfrac{8}{9}×\dfrac{5}{18}×\dfrac{9}{10}&=\dfrac{8^4\hspace{-6mm}\color{darkred}{\setminus}}{9^1\hspace{-6mm}\color{darkred}{\setminus}}×\dfrac{5^1\hspace{-6mm}\color{darkred}{\setminus}}{18}×\dfrac{9^1\hspace{-6mm}\color{darkred}{\setminus}}{10^2\hspace{-6mm}\color{darkred}{\setminus}}\\\\ &=\dfrac{4^2\hspace{-6mm}\color{darkred}{\setminus}}{18^9\hspace{-7mm}\color{darkred}{\setminus}}\\\\ &=\dfrac{2}{9}\end{align}