![]()
Equivalent fractions
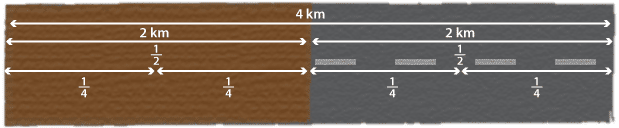
If 2 kilometres of a 4-kilometre road is sealed, we say that \(\dfrac{2}{4}\) (two quarters) of the road is surfaced. We also know that this means \(\dfrac{1}{2}\) (half) is sealed. The fractions \(\dfrac{2}{4}\) and \(\dfrac{1}{2}\) are called equivalent fractions and we write \(\dfrac{2}{4}=\dfrac{1}{2}\).
Using a number line
We can say two fractions are equivalent if they are represented by the same marker on a number line.
To show that, for example, \(\dfrac{1}{2}=\dfrac{3}{6}\) , draw a number line and mark 0 and 1. Form two intervals of equal length from 0 to \(\dfrac{1}{2}\) and from \(\dfrac{1}{2}\) to 1. Each interval has a length of \(\dfrac{1}{2}\).
![]()
Now divide each of these intervals into three equal subintervals to form six in total. Each of these intervals has a length of \(\dfrac{1}{6}\).
The markers \(\dfrac{1}{2}\) and \(\dfrac{3}{6}\) are at the same point on the number line so \(\dfrac{1}{2}\) and \(\dfrac{3}{6}\) are equivalent.





