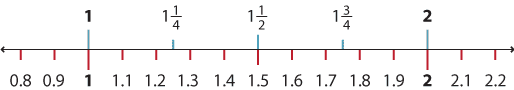![]()
Connecting fractions and decimals
Decimals are a useful way of writing fractions with denominators of 10, 100, 1000 and so on. For example:
\(\dfrac{4}{10}=0.4, \dfrac{6}{100}=0.06, \dfrac{83}{100}=0.83\) and \(\dfrac{269}{1000}=0.269\).
Decimal numbers use the decimal fractions \(\dfrac{1}{10}, \dfrac{1}{100}, \dfrac{1}{1000}\) and so on, along with the whole numbers. When you say the decimal using its place value, it is easy to write the fraction. For example, 0.7 = seven tenths = \(\dfrac{7}{10}\).
The number 34.795 can be read as thirty-four and seven hundred and ninety-five thousandths, which is the same as \(34\dfrac{795}{1000}\). It can also be read as three tens, four ones, seven tenths, nine hundredths and five thousandths or \(30 + 4 + \dfrac{7}{10} + \dfrac{9}{100} + \dfrac{5}{1000}=34\dfrac{795}{1000}\).
Students need to know the common fractions and their equivalent decimals including:
\(\dfrac{1}{8}=0.125\hspace{10mm}\dfrac{1}{4}= 0.25\hspace{10mm}\dfrac{3}{8}=0.375\hspace{10mm}\dfrac{1}{2}=0.5\hspace{10mm}\dfrac{5}{8}=0.625\hspace{10mm}\dfrac{3}{4}=0.75\)
Converting fractions to decimals
To convert from fractions to decimals, we first convert the fraction we are working with to a fraction with a denominator that is a power of ten.
If we start with \(\dfrac{1}{4}\), what equivalent decimal fraction can we make? We cannot multiply the denominator by a whole number to get 10. We can multiply the denominator by 25 to get 100. So we must also multiply the numerator by 25 to get \(\dfrac{25}{100}\) as our new fraction. Now we can write this as a decimal.
\(\dfrac{1}{4}=\dfrac{25}{100}=0.25\)
To calculate the decimal from the fraction \(\dfrac{1}{2}\), we need to find an equivalent decimal fraction. We can multiply the denominator by 5 to get 10. So we must also multiply the numerator by 5 to get \(\dfrac{5}{10}\).
\(\dfrac{1}{2}=\dfrac{5}{10}=0.5\)
Another way of calculating a decimal from a fraction is to divide the numerator by the denominator.
For example, to convert \(\dfrac{3}{4}\) to a decimal, divide 3 by 4 using the division algorithm.
\(\hspace{3mm}\dfrac{0.75}{\hspace{-3mm}4\big)3.^30^2}\\ \dfrac{3}{4}=0.75\)
The use of a number line to demonstrate the equivalence of fractions and decimals can also be helpful.