Multiplication algorithm

The multiplication algorithm is a series of steps we use to multiply numbers that are too difficult to multiply mentally. In the early years of school students will practise this method with quite simple numbers.

The distributive property for multiplication is central to our multiplication algorithm because it enables us to calculate products one column at a time and then add the results together. The distributive property involves splitting the numbers into parts and then multiplying the parts.

For example, using the distributive law we calculate:

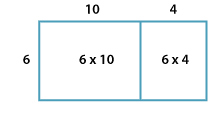
\begin{align*} 6\times14 &= 6\times10+6\times4\\\\ &= 60+24\\\\ &= 84\\\\ \end{align*}

We can show this as a picture, using areas to represent each number:

Detailed description

We can also use the multiplication algorithm:

	1	4
×	\(\ \ _2\)	6
	8	4

To multiply 23 × 17 we follow these steps:

• Set out the numbers so the digits line up according to their place value.
• Start with the ones. Multiply the ones digit in 17 by the ones digit in 23. Say '7 times 3 is 21'. Write '1' in the ones column and carry '2' to the tens column.
• Next, work with the tens. Multiply the ones digit in 17 by the tens digit in 23.
• Say '7 times 2 is 14'. Add the '2' carried from before. Write '6' in the tens column and a '1' in the hundreds column.
• Now multiply the tens digit in 17 by the ones digit in 23. This will give a certain number of tens, so start by writing '0' in the ones column. Say '1 times 3 is 3'. Write '3' in the tens column.
• Next, multiply the tens digit in 17 by the tens digit in 23. Say '1 times 2 is 2'. Write '2' in the hundreds column.
• Finally, add 161 to 230.

The product of 23 × 17 is 391.

	Hundreds	Tens	Ones
		\(2_2\)	3
×		\(1\  \)	7
	1	\(6\  \)	1
	2	\(3\ \)	0
	3	\(9\  \)	1