Simple addition

The basis of all addition is the ability to add two single-digit numbers. You should be fluent with all single-digit addition as shown in the following diagram. Fluency in this case means the ability to instantly recall these 'number facts' without having to start from scratch and add them mentally or resort to using fingers to add.

+	0	1	2	3	4	5	6	7	8	9
0	0	1	2	3	4	5	6	7	8	9
1	1	2	3	4	5	6	7	8	9	10
2	2	3	4	5	6	7	8	9	10	11
3	3	4	5	6	7	8	9	10	11	12
4	4	5	6	7	8	9	10	11	12	13
5	5	6	7	8	9	10	11	12	13	14
6	6	7	8	9	10	11	12	13	14	15
7	7	8	9	10	11	12	13	14	15	16
8	8	9	10	11	12	13	14	15	16	17
9	9	10	11	12	13	14	15	16	17	18

There are a number of useful strategies for addition. Many of these can be done mentally or are useful pencil and paper strategies. You will need to begin assessing strategies for efficiency and selecting the most efficient for the purpose. Many of the strategies can be learned with small numbers and extended for use with large numbers.

Doubles and near doubles

It is useful to be able to swiftly recall doubles of numbers up to 100. Near doubles include additions within one or two of the double.

For example, to calculate 36 + 36, we double 36 to get 72. For 36 + 37, we double 36 to get 72 and add 1.

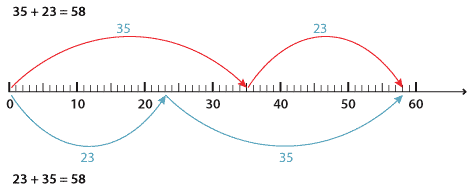
Order does not matter for addition

When doing addition, the order in which we add the numbers does not matter. For example:

Detailed description

This also works for three or more numbers and can be used to arrange numbers so that they are easily added.

For example:

\begin{align*} 11+27+16+9+13 &=27+13+11+9+16\\\\ &=40+20+16\\\\ &=76 \end{align*}

Make up to a ten

Take some of one number and add it to the other number to make up a ten or a multiple of ten.

For example:

\begin{align*} 19+37 &=20+36\\\\ &=56 \end{align*}

Add from the left

We can add from the left, starting with the largest parts. Add the digits with the same place value beginning from the left. This is a handy mental strategy.
For example:

\begin{align*} 867+395+109 &=800+300+100+60+90+7+5+9\\\\ &=1200+150+21\\\\ &=1371 \end{align*}

Compensation

Add more than you need and then subtract the extra that you added on.
For example:

\begin{align*} 289+397 &=289+400-3\\\\ &=689-3\\\\ &=686 \end{align*}