Content description

Choose appropriate units of measurement for length, area, volume, capacity and mass (ACMMG108)

Calculate perimeter and area of rectangles using familiar metric units (ACMMG109)

Source: Australian Curriculum, Assessment and Reporting Authority (ACARA)

Area of rectangles

The area of a rectangle is the size of the region inside it.

For this rectangle, drawn on centimetre grid paper, the area is 18 square centimetres. We can write square centimetres as cm².

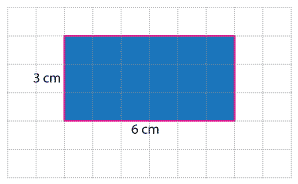
We can find the area of a rectangle by multiplying its length by its width.

We know the lengths of the sides of the rectangle above, and can use this to calculate its area. A 6 cm by 3 cm rectangle contains 6 × 3 = 18 squares, each with an area of 1 square centimetre. So the area of the rectangle is 18 square centimetres, or 18 cm².

We usually set this out as follows:

\begin{align}\text{Area} &= \text{length}\ ×\ \text{width}\\ &= 6 × 3\\&= 18\ \text{cm²}\end{align}

We call this the formula for calculating the area of rectangles, and write it as:

\begin{align}\text{Area}\ &= \text{length}\ ×\ \text{width}.\end{align}

When we are working with squares we can use the properties of a square to calculate its area. Since the side lengths of the square are equal, the formula becomes:

Area = length × length.

So for the square above:

\begin{align}\text{Area}\ &= 8 × 8\\&= 64\ \text{km²}\end{align}