Links Forward

Isometries

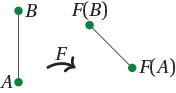
An isometry is a plane transformation which preserves lengths. That is, a plane transformation $F: \mathbb{R}^2 \rightarrow \mathbb{R}^2$ is an isometry if, for any points $A$ and $B$ in the plane, the distance between $A$ and $B$ equals the distance between $F(A)$ and $F(B)$.

Isometries are important types of transformations, as they preserve geometry. All lengths must remain the same, and hence angles and areas must also remain the same.

Some of the transformations we have seen are isometries, and others are not.

Lemma

Any rotation is an isometry. That is, for any point $P$ and any angle $\theta$, $\text{Rot}_{P, \theta}$ is an isometry.

Proof

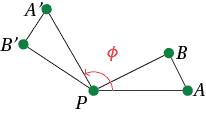
Take two distinct points $A$ and $B$. Let $A',B'$ be their images under rotation. We must show $AB = A'B'$.

Suppose $A,B$ are distinct from $P$. Consider triangles $PAB$ and $PA'B'$. As $A'$ is obtained from $A$ by a rotation about $P$, $PA = PA'$. Similarly $PB = PB'$. Since $A',B'$ are obtained by rotating $A,B$ by $\phi$ about $P$, $\angle APB = \angle A'PB'$. Hence $\triangle PAB \cong \triangle PA'B'$, so $AB = A'B'$.

In the case $A=P$, we have $A' = P$ so $PB = PB'$ implies $AB = A'B'$. The case $B=P$ is similar.

$\Box$

Exercise 41

Show that any translation or reflection is an isometry, but that any projection onto a line, or dilation from a line by factor $k \neq \pm 1$ is not an isometry.

An isometry must preserve areas, so if we have an isometry which is a linear transformation corresponding to a matrix $M$, then $\det M = \pm 1$. However, the converse is not true. There are transformations which preserve areas, but which are not isometries.

Exercise 42

Let $M = \begin{bmatrix} 2 & 0 \\ 0 & \frac{1}{2} \end{bmatrix}$. Show that $T_M$ preserves areas, but is not an isometry.

If you compose two isometries, the result must be another isometry. It is interesting to think abut what you get by composing various types of isometries.

For instance, composing a reflection in $L$ with itself results in the identity. But what if we take two reflections in different lines $L_1$ and $L_2$?

Example

Let $L_1$ be the line $x=0$, and $L_2$ the line $x=d$. Show that reflection in $L_1$ followed by $L_2$ is translation by $(2d,0)$.

Solution

We note that $\text{Ref}_{L_1} (x,y) = (-x,y)$ and $\text{Ref}_{L_2} (x,y) = (2d-x,y)$ (see exercise 26), so

\[ \text{Ref}_{L_2} \circ \text{Ref}_{L_1} (x,y) = \text{Ref}_{L_2} (-x,y) = (x+2d,y) = (x,y) + (2d,0), \]

which is translation by $(2d,0)$.

In general, if $L_1$ and $L_2$ are parallel, distance $d$ apart, then the composition $\text{Ref}_{L_2} \circ \text{Ref}_{L_1}$ is a translation by distance $2d$ in a direction perpendicular to $L_1$ and $L_2$.

What if $L_1$ and $L_2$ intersect at a point $P$? Then it turns out that reflection in $L_1$, followed by reflection in $L_2$, gives a rotation.

Example

Let $L_1$ be the $x$-axis and $L_2$ the line through the origin making an angle of $\phi$ with the $x$-axis. Show $\text{Ref}_{L_2} \circ \text{Ref}_{L_1}$ is a rotation, and find its angle.

Solution

Denote points by polar coordinates $(r, \theta)$. Then reflection in $L_1$ sends a point $(r,\theta)$ to $(r,-\theta)$, and reflection in $L_2$ sends $(r,\theta)$ to $(r, 2\phi - \theta)$. Performing the two reflections in order sends $(r,\theta) \mapsto (r,-\theta) \mapsto (r,\theta + 2\phi)$. So the composition is a rotation by angle $2\phi$ about the origin:

\[ \text{Ref}_{L_2} \circ \text{Ref}_{L_1} = \text{Rot}_{{\bf 0}, \; 2\phi}. \]

Exercise 43

Give an alternative proof of this statement by showing that the product of the matrices for reflection in $L_1$ and $L_2$ is a rotation matrix of angle $2\phi$.

If you compose a translation of some distance along a line $L$, with reflection in $L$, you obtain a type of isometry known as a glide reflection.

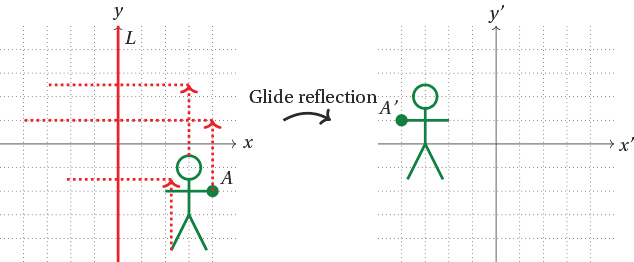
We have now seen many examples of isometries: rotations, translations reflections, glide reflections, and the identity. We might ask if there are any others. The following theorem says that there are not: we have now seen them all.

Theorem (Classification of isometries of the plane)

Suppose $F: \mathbb{R}^2 \rightarrow \mathbb{R}^2$ is an isometry. Then $F$ is a rotation, translation, reflection, glide reflection or the identity.

We will not prove this theorem. A proof can be found, for instance, in I. M. Yaglom, Geometric Transformations I.

Next page - Links Forward - Three-dimensional and higher-dimensional transformations