Links Forward

Areas and determinants

The determinant of a $2 \times 2$ matrix is given by

\[ \det \begin{bmatrix} a & b \\ c & d \end{bmatrix} = ad - bc. \]

The determinant has a nice geometric interpretation in terms of areas, and this interpretation can also be applied to linear transformations.

We discussed earlier (in "The effect of a linear transformation") how two vectors ${\bf v}$ and ${\bf w}$ can be used to construct a parallelogram, the parallelogram spanned by ${\bf v}$ and ${\bf w}$. We discussed how, if the matrix $M = \begin{bmatrix} {\bf v} & {\bf w} \end{bmatrix}$ has ${\bf v}$ and ${\bf w}$ as its columns, then the linear transformation $T_M$ sends the unit square to this parallelogram. We also discussed the orientation of this parallelogram and how $T_M$ can preserve or reverse orientation.

We now ask: what is the area of this parallelogram? It is closely related to the determinant of the matrix $M$.

For instance, if ${\bf v} = (1,0)$ and ${\bf w} = (0,1)$, then ${\bf v}$ and ${\bf w}$ span the unit square, and these two vectors form the matrix

\[ M = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, \quad \text{which has determinant $1$.} \]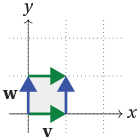

Similarly, if ${\bf v} = (2,0)$ and ${\bf w} = (3,-5)$, then we obtain a parallelogram with base length $2$ and height $5$, hence with area $10$; and the corresponding matrix is

\[ M = \begin{bmatrix} 2 & 3 \\ 0 & -5 \end{bmatrix}, \quad \text{which has determinant $-10$.} \]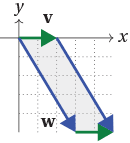

The determinant equals the negative area. But in this case the parallelogram is negatively oriented and the linear transformation reverses orientation.

In fact, the determinant of $M = \begin{bmatrix} {\bf v} & {\bf w} \end{bmatrix}$ gives the signed area of the parallelogram spanned by ${\bf v}$ and ${\bf w}$, i.e. positive or negative area according to orientation.

The linear transformation $T_M$ sends the unit square to this parallelogram, and in fact takes the tessellation of the plane by unit squares by a tessellation by these parallelograms. So unit squares of area $1$ are taken to parallelograms of signed area $\det M$. Thus $T_M$ expands areas by a factor of $|\det M|$, and preserves or reverses orientation accordingly as $\det M$ is positive or negative. For any region $R$ in the plane, its image $T_M (R)$ under $T_M$ has area $|\det M|$ times the area of $R$.

Exercise 38

In this exercise we prove that, if $M = \begin{bmatrix} {\bf v} & {\bf w} \end{bmatrix}$, then $\det M$ is signed area of the parallelogram spanned by ${\bf v}$ and ${\bf w}$. Let $A({\bf v}, {\bf w})$ be this signed area.

Show that for any real number $k$, $A({\bf v}, {\bf w}) = A({\bf v}, {\bf w} + k{\bf v})$ and $A({\bf v}, {\bf w}) = A({\bf v} + k {\bf w}, {\bf w})$.
Show that $A({\bf v}, {\bf w}) = -A({\bf w}, {\bf v})$.
Show that $A \left( \begin{bmatrix} a \\ 0 \end{bmatrix}, \begin{bmatrix} b \\ d \end{bmatrix} \right) = ad$ and $A \left( \begin{bmatrix} a \\ c \end{bmatrix}, \begin{bmatrix} b \\ 0 \end{bmatrix} \right) = -bc$.
Show that, if $d \neq 0$, then $A \left( \begin{bmatrix} a \\ c \end{bmatrix}, \begin{bmatrix} b \\ d \end{bmatrix} \right) = A \left( \begin{bmatrix} a - \frac{bc}{d} \\ 0 \end{bmatrix}, \begin{bmatrix} b \\ d \end{bmatrix} \right) = ad -bc$.
Conclude that $A({\bf v}, {\bf w}) = \det M$, where $M = \begin{bmatrix} {\bf v} & {\bf w} \end{bmatrix}$.

Example

Find the determinant of the matrix corresponding to the rotation $\text{Rot}_{{\bf 0}, \frac{\pi}{3}}$ of $\pi/3$ about the origin, and explain what this means for areas and orientations.

Solution

The corresponding rotation matrix (with $\phi = \pi/3$) is

\[ M = \begin{bmatrix} \cos \phi & -\sin \phi \\ \sin \phi & \cos \phi \end{bmatrix} = \begin{bmatrix} \frac{1}{2} & \frac{\sqrt{3}}{2} \\ - \frac{\sqrt{3}}{2} & \frac{1}{2} \end{bmatrix}, \quad \text{which has} \quad \det M = %\frac{1}{2} \cdot \frac{1}{2} - \frac{\sqrt{3}}{2} \cdot \left( - \frac{\sqrt{3}}{2} \right) = \frac{1}{4} + \frac{3}{4} = 1. \]

Thus the linear transformation $\text{Rot}_{{\bf 0}, \pi/3}$ preserves areas and orientations.

In fact, any rotation preserves areas, so any rotation matrix has determinant 1. Similarly, reflections preserve area, but reverse orientation, so reflection matrices have determinant $-1$. Projections collapse all areas down to zero, so have determinant zero.

Exercise 39

Prove these facts. Show any rotation matrix has determinant $1$, any projection matrix has determinant $0$, and any reflection matrix has determinant $-1$.

What about dilation? Dilation from a line $L$ by factor $k$ expands lengths by a factor of $k$ in the direction perpendicular to $L$, but leaves lengths unchanged in the direction of $L$. Thus, areas expand by a factor of $k$.

Example

Let $L$ be the line $y=x$. Find the determinant of the matrix corresponding to dilation from $L$ by a factor of $3$. Explain what this means for areas and orientations.

Solution

Using the formula for a dilation matrix, with $k=3$ and $\phi = \pi/4$, $\text{Dil}_{L,3}$ has matrix

\[ \begin{bmatrix} 1 + (k-1) \sin^2 \phi & (1-k) \sin \phi \cos \phi \\ (1-k) \sin \phi \cos \phi & 1 + (k-1) \cos^2 \phi \end{bmatrix} = \begin{bmatrix} 2 & -1 \\ -1 & 2 \end{bmatrix} \quad \text{which has determinant 3.} \]

Hence $\text{Dil}_{L,k}$ expands areas by a factor of $3$, and preserves orientation.

Exercise 40

Show that the determinant of a general dilation matrix is $k$.

Next page - Links Forward - Isometries