Content

A Reasoning Retreat

There used to be an advert that talked about 'the pause that refreshes'. This section is meant to be a refreshing reasoning pause. Its aim is to give a background to reasoning before we start on the more serious business looking at truth.

Reasoning is a fundamental human process. Very little is achieved in life without thinking that involves reasoning even at the level of deciding whether the pair of shoes we have just put on our feet is what we would like to purchase or not. (If we buy this could we wear it with this on such and such occasions?) And it's not unknown in animals even. (If I fetch this stick I'll probably get a nice biscuit.) Certainly the first Australian Raven (Crow) who discovered how to eat a Cane Toad without dying of the toad's poison almost certainly gave the matter some thought.

Now there are several types of reasoning that we commonly use. These are discussed in more depth in Holton, D., Stacey, K., & FitzSimons, G. (2012). Reasoning: A dog's tale. The Australian Mathematics Teacher, 68(3), 22-26.

The main type of reasoning for the purposes of this module is deduction (https://en.wikipedia.org/wiki/Deductive_reasoning). This is the 'if $ \dots$ then' procedure that is required in mathematics all the time. It can be seen in alternate forms that either involve 'if' or 'then', 'this implies that' or use 'because', 'so' and the like, or any of these implicitly. This form of reasoning involves some statement, proposition, and some rule. If the statement holds then the rule allows us to make a true conclusion. 'Because these lines are parallel and this angle is $30^{\circ}$, then this other angle is $30^{\circ}$.' This is an example where corresponding angles are involved and there is a rule about corresponding angles that enables us to make a deduction.

Given a true, valid, proposition and a proven rule, deduction will give a correct result.

But other ways of reasoning are not so tight and predictable. We'll consider two of these. First let's look at the detective's method. Someone has been murdered with a knife. Jake has a bloodstained knife in his pocket (proposition). So Jake is the murderer. But poor old Jake has just been taking a stone out of his horse's hoof, the knife slipped and he cut himself. In the second scene of the TV programme someone checks the DNA of the blood and Jake is released though maybe he actually used another knife for killing. There is likely to be a knife somewhere with at least a minute amount of blood on it and it will probably be found before the end of the next 120 minutes.

This kind of reasoning is called abduction (https://en.wikipedia.org/wiki/Abductive_reasoning) and is used a lot especially when we think we are using deduction. 'If Jake has a knife, then he killed the victim' is a deduction but it relies on the rule that 'someone who has a knife may have killed the victim'.

It turns out that much of the false reasoning that we do is based on abduction. With an apology to Socrates, let's look at 'all men are liars', 'Helen is a liar', so 'Helen is a man'. Again we are putting things the wrong way round and getting a false conclusion (although there is a Johnny Cash song about a boy named Sue!)

However, abduction has its uses in mathematics. It is a very good source for ideas. We observe something. That observation leads to a conclusion under a certain rule. That conclusion may be true or false but it might be true and it might lead us to some new ideas and new ways to approach old ideas.

Then there is the data collection method that finds a pattern for the data collected. This leads to the pattern being assumed for all situations. But sometimes this conclusion is false. The regions problem works this way. Take a circle and choose some points on its boundary. In joining up all the points with straight lines you produce a number of regions (see Figure 6). The number of regions appears to double as the number of points increases. This is certainly what the data up to 6 points suggests. However, it all goes horribly wrong with 6 points.

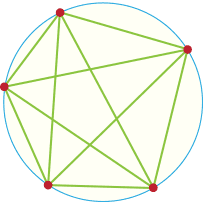
Figure 6: Regions formed in a circle

Again this is a method we all use all of the time. Sometimes this works for every case; sometimes, as in the regions problem, it doesn't. Whichever way it is food for thought and possibly new ideas. If it is true we need to prove it; if it is false we need to find a counterexample. Either way might be useful.

The kind of reasoning used here is called induction. (https://en.wikipedia.org/wiki/Inductive_reasoning)

(This is not to be confused with Mathematical Induction which is a well-established and valuable even valid proof method.) Like abduction, induction is a great way to produce new ideas and, possibly, new results in mathematics.

But sometimes we reason incorrectly by looking at the converse of an implication, a deduction. But let's take a maths example. If you are stacking cans as in Figure 6, with one less can in each row as you move up the stack, you can easily show that if a stack has seven rows, the number of cans in the stack is divisible by 7. This can be done by letting the top row have $m$ cans, the next have $m + 1$, and so on. Then the number of cans is $m + (m + 1) + (m + 2) + \cdots+ (m + 6) = 7m + 21$. In the heat of the moment you might think that if a number is divisible by 7, then that number of cans can be stacked in seven rows. In this case though this converse of the original correct implication is false. The only way you can stack 14 cans is shown in Figure 7. However, looking at the converse we might get some useful ideas about stacking cans.

Figure 7: Stacking 14 cans

In the next section we'll concentrate on deduction and related issues. However it is worth knowing that this is not the only way that we reason and to know the value of each type of reasoning. Deduction gives watertight results. Abduction and induction give new ideas that have to be tested before they can be trusted.

Having got that off our chests we can now get on with the serious things of life such as propositional logic.

Next page - Content - Propositions