Content

Switches again

Now you should be worrying about whether this Boolean algebra has anything to do with switches at all. In the section on switches we saw that we had a `$+$' and a `$\times$', which were defined in terms of the parallel and series organisation of switches. Given that the 0 and 1 of the smallest Boolean algebra developed from switches, it seems natural to worry about whether switching circuits satisfy the axioms of a Boolean algebra. Let's work through them to see if any fail.

• Axiom 1

  The switches contain the elements 0 , no switches and 1, the line is always open.li>
  So that looks OK, if a bit fudged.

• Axiom 2

  $B$ is closed under $+$ and $\times$. That is for all $x$ and $y$ in $B$, $x + y$ and $xy$ are in$ B$. Certainly if x and y are two switches we can put them in parallel and series to get another switching object.

• Axiom 3

  + and x are commutative. That is for all $x$ and $y$ in $B$, $x + y = y + x$ and $xy = yx$. The arrangement of the parallel pieces or the series pieces is irrelevant so this axiom is satisfied.

• Axiom 4

  + and $\times$ are associative. That is, for all $x, y$ and $z$ in $B$, $(x + y) + z = x + (y + z)$ and $(xy)z = x(yz)$. Again order is unimportant for switch arrangements.

• Axiom 5

  $\times$ is distributive over + and + is distributive over $\times$. That is, for all $x, y$ and $z$ in $B$, $x(y + z) = xy + xz$, while $x + yz = (x + y)(x + z).$
  Now the best way to check these is to use a table, see Table 4 below.
  

  Table 4: A proof that $x(y+z)=xy+xz$

  $x$	$y$	$z$	$x(y+z)$	$xy+xz$
  0	0	0	0	0
  0	0	1	0	0
  0	1	0	0	0
  0	1	1	0	0
  1	0	0	0	0
  1	0	1	1	1
  1	1	0	1	1
  1	1	1	1	1

  
  We leave the second part of this checking to the Questions below.

• Axiom 6

  + and $\times$ have identities in $B$ which are denoted, respectively, by 0 and 1. That is for all $x$ in $B$, $x + 0 = x$ and $x \times 1 = x$.
  If we put a wire with no switches in parallel with no switch we get the same result as having just the switch. We leave the second of these to the Questions below.

• Axiom 7

  + and $\times$ obey two absorption laws. That is, for all $x$ and $y$ in $B$, $x + x \times y = x$ and $x(x + y) = x.$
  A proof of these is left to the Questions below.

• Axiom 8

  + and $\times$ both have a common complement. That is, for all $x$ in $B$, there is an $x'$ in $B$ such that $x + x' = 1$ and $xx' = 0$.

This is just the way that parallel and series switching works for $x$ and its complement.

We now have all the axioms of a Boolean algebra, so a set of switches joined in parallel and series forms a Boolean algebra. BUT, what use is this?

Let's consider an example. Recall Q3, Voting for Three of the 'Light in the Passage' section (see page 8). We have to set up switches so that a light goes on when two people out of three vote for an option by switching their switches on. Let $x$, $y$ and $z$ be the three options. Then $xy + xz + xz + xyz$ will give us a perfectly good switching system. However, we can simplify this using the properties of Boolean algebra.

$xy + xz + yz + xyz = x(y + z) + yz(1 + x) = x(y +z) + yz$.

This produces the switching system of Figure 5.

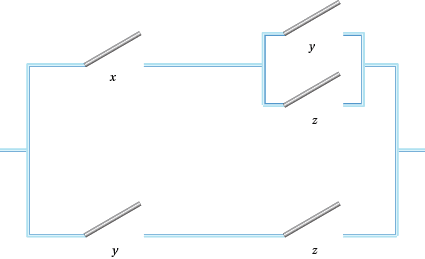
Figure 5:A switching circuit for voting for three

For what it's worth, this switching set up requires one less switch than the number needed using the obvious alternative arrangement of $xy + xz + yz.$

Next page - Content - Functions for Boolean Algebras