Content
Gates
Given propositional logic and switching circuits are related via Boolean algebra it makes sense to see if we can automate operations in logic through circuits. When you think about it $p + q$ must be linked in parallel as we need both propositions to be true in order for $p + q$ to be true. In the same way $pq$ should be a parallel connection.
Questions
- Find a logic circuit for $p \to q$.
- Draw circuits for $q(p + q)$ and $p + pq$ and show that they are equivalent using two methods.
But logic circuits have a simplification that doesn't occur in switching circuits. This is the concept of gates that will do for specific jobs. So we have AND gates, OR gates, NAND gates NOR gates and NOT gates. Let's take these one at a time.
AND gates
These represent the 'both and' operation in logic. In the simplest case the inputs are $p$ and $q$ and the outputs$ pq$.
However, to deal with a number of proposition, we may have inputs $p, q, ., r $and outputs $pq\dots r$.
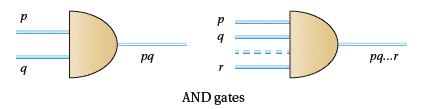
Figure 8a: AND gates
NAND gates
These provide the negation of AND gates. So inputs $p, q, \dots, r$ produce outputs $p'q'\dots r'$
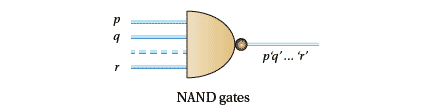
Figure 8b: NAND gates
Or gates
As you might expect, the inputs for OR gates are $p, q, \dots,r$ and the outputs $p + q + \cdots + r$.
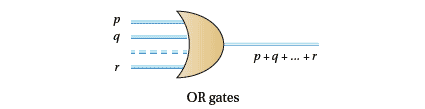
Figure 8c: OR gates
NOR gates
Here we have the negation of OR to give outputs of $(p + q + \cdots + r)'$
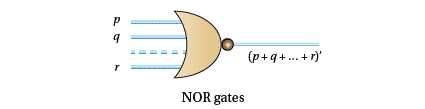
Figure 8d: NOR gates
NOT gates
These are for negation. So$ p$ goes in and $p'$ comes out.
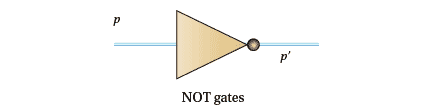
Figure 8e: NOT gates
These gates allow a considerable reduction in the diagrams necessary to produce the corresponding logic circuits. As well as that they are on tap for actually constructing the logic circuits themselves.
Questions
- Produce logic circuits for the logical expressions below. Then represent these using the gates of Figure 8.
- $(p'q)'+ r$;
- $((pq)'r + s)(pq + r's)$.
- What proposition does the following gate diagrams represent?

Figure 9a: Question 61
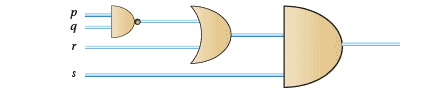
Figure 9b: Question 61
Search engine queries also employ the logic gates we have been considering. To do this searching, each web page on the Internet can be thought of as an 'element' of a 'set'. Elements in this set that are combined with a space between them are accepted as being connected by AND. So typing 'blue dogs' should get you sites where the words 'blue' and 'dogs' are next to each other.
On the other hand 'blue OR dogs' should give you sites that contain either 'blue' or 'dogs'.
If you are looking for blue objects that are not dogs you should get this by using 'blue NOT dogs'. Alternatively you can insert a minus sign before the second word (or phrase) as in 'blue-dogs' (with no space between the minus sign and the second object.
