Content

Lights in the Passage

The passage to our front door is lit by a light that is controlled by two switches, one at either end. When you switch a light on at one end you can switch it off from that same end or from the other end. This has obvious advantages for both human and electrical efficiency. But how would you wire such an arrangement?

Well, it's clearly not in series as we've shown in Figure 1, where the switches x and y are joined `in line'.

Figure 1: Two switches in series

Given the series set up you would need both $x$ and $y$ to be `on' to get the light to work. Any other positioning of the switches would lead to no light which isn't so good if you've just come home to a dark house and you don't want to fall over the cat. Just to emphasise this, we've drawn up Table 1. By `on' for a switch we visualise it as making a connection with the `wire' shown in Figure 1.

Table 1: The effect of two switches in series
Switch $x$ Switch $y$ Light
on on on
on off off
off on off
off off off

That's obviously not how the electrician wired up the hall light. So the next guess is a wiring that is in parallel (see Figure 2).

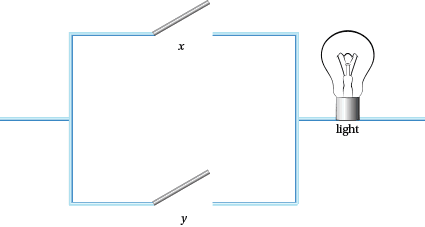
Figure 2: Two switches in parallel

All the possible situations are show in Table 2, but this is no good either because, for example, when $x$ is on, the light is always on.

Table 2: The effect of two switches in parallel
Switch $x$ Switch $y$ Light
on on on
on off on
off on on
off off off

Now the only ways to wire things together are in series or parallel. So how did the electrician wire up the passage?

Questions

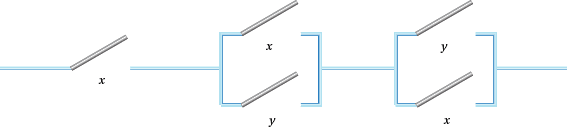
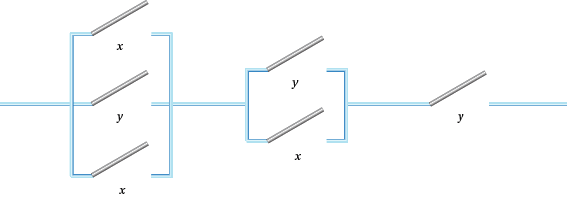
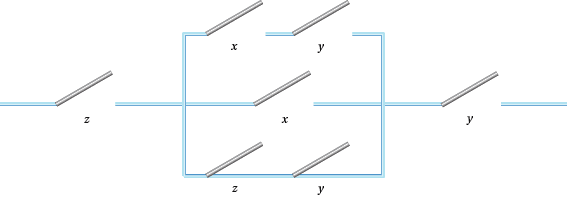
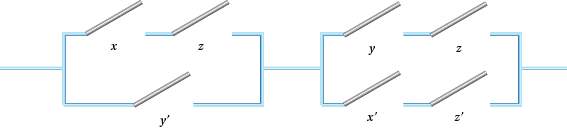
  1. Draw up a table of off and on results for the switches in the circuits in Figure 3. Simplify the circuits where possible.

Figure 3: Some switching circuits

Questions

  1. Voting for Two: Jamal and John have invented a system for getting a majority vote. If they both vote `yes' by pressing a button a light comes on. Otherwise there is no light. Draw up a table that explains this system. What does this simplify to?
  2. Voting for Three: Veronique joins Jamal's and John's committee. Draw up a table for a system that produces a light only when there is a majority vote. What does this simplify to?
  3. Passage Problem: Assume that switches $x$ and $y$ both start in the off position and the light is then off too. Draw up a table of the results we want to achieve so that we get the desired effect in the passage.
  4. Experiment with circuits that are combinations of two switches used in a variety of series and parallel arrangements. Produce on, off tables for each of them.

As we shall see shortly there are advantages to replacing the on and off of switches by 1 and 0. This means that Table 1 would become Table $1'$.

Table $1'$: The effect of two switches in series using ones and zeros
Switch $x$ Switch $y$ Light
1 1 1
1 0 0
0 1 0
0 0 0

Questions

  1. In all the tables you have met so far, replace on and off with 1 and 0.
  2. Table 1$' $ looks like multiplication. We could replace the whole of the table, and therefore the whole series system, by $x \times y$. What algebraic expression could you replace the parallel arrangement of switches by?
  3. But the arithmetic here is a little strange. In particular what is 1 + 1 in the parallel case? Where else in mathematics does this kind of thing happen?
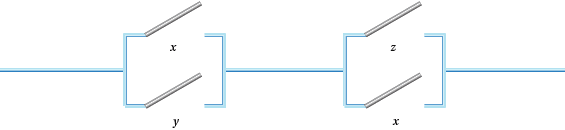
  4. Think about the tables in Q6 from an algebraic standpoint. Can you express the results algebraically in terms of $x, y$ and $z$?

One final device that is useful here is the complement $x'$ of a switch $x$. The effect of this is shown in Table 3. The idea here is that when $x$ switch is on, its complement is off and vice versa.

Table 3: The complement of a switch
Switch $x$ Switch $x'$
1 0
0 1

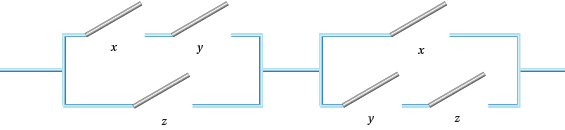
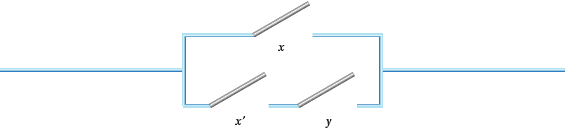
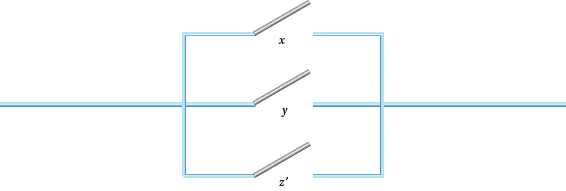
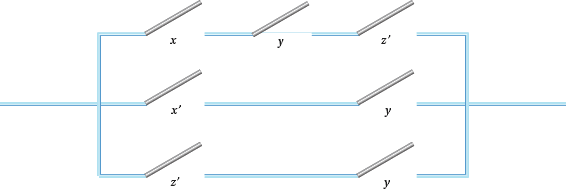
Figure 4: Some switching circuits

Questions

  1. Draw up 0 and 1 tables for the circuits in Figure 4. Produce algebraic expressions for each of them in terms of the $+$ and $\times$ of parallel and series switches.
  2. Now try to algebraicise the Passage Problem of Q4.
  3. Continue to experiment as in Q5, but now allow for a switch and/or its complement to be present.

Next page - Content - Boolean Algebra 2