Answers to questions

Question 1

Unfortunately no. You can do this by trial and error on Figure 3. But it will help to alter Figure 3 slightly in the following way. Put a dot on every land mass and join two dots by a line for each bridge that connects them. So we get Figure A1 below. And then it would help to think a little more deeply than trial and error.

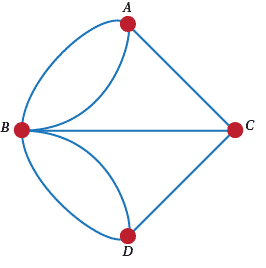
Figure A1: Königsberg reduced to dots and lines

Suppose that you could do the round trip walk. And suppose that you started at land mass A. Then you would have to go out from A on a bridge. So you start by using one bridge. At any time later that you came back to A you would use one bridge going in to A and one edge going out. So far you have used an odd number of bridges. Eventually you'll go back to A and use one final bridge to make the bridge count even. BUT! No land mass is attached to an even number of bridges. SO! There is no round trip walk.

Question 2

Apply the argument of Q1 to show that every land mass, except for the initial and final one, has to be attached to an even number of bridges. So can you see why the answer here is `no' too?

Question 3

It turns out that, over time, Königsberg in Prussia has become Kaliningrad, Russia. In the process of time, the seven bridges have been reduced to five. If the current position of the bridges is as shown in Figure A2, then the walk ($A, B, C, D, B, A$) can be done.

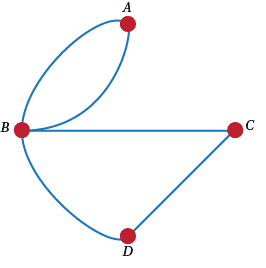
Figure A2: A walk with five bridges

How did you go with six bridges? Can you only find a walk that starts on one part of the city and ends up somewhere else? Why?

Question 4

Yes, put in two landmasses $X$ and $Y$ between $C$ and $D$ and then $A, B, C, D, X, Y, B A$ will get you round. But can you be more imaginative than that?

Question 5

Well it just depends on how you deploy your bridges. Sometimes there is a round trip walk and sometimes there ain't. What is the important feature that will guarantee a walk?

Question 6

The key point is the even-ness of the number of bridges at each land mass. Is it possible to prove that if the number of bridges at each land mass is even, then there is a round trip walk? Is it possible to show that if there is a round trip walk, then the number of bridges at each land mass is even? So is it true that there is a round trip walk if and only if the number of bridges at each land mass is even? Can you prove this? Beware the lure of a simple result. Make sure that you carefully word your answer. (See Euler's Tour Theorem.)

Question 7

The answer is no, but we'll get back to this later when we've thought about 'planarity' and $K_3$ - whatever they are.

Question 8

Putting one dot on the page should give a graph with one vertex, so A is not a possibility. How could we have more than one graph though? Perhaps we could have differently shaped vertices? No, we will assume that however you draw the vertices they are the same vertex (though we usually draw them as small circles). So what else could we do? There is the possibility of edges. Could we draw an edge from a vertex to a vertex? There seems to be nothing in the rules to stop that. Such things are called loops. We show one in Figure A3.

Figure A3: A graph with a loop

Those of you who wanted to include loops would have answered D to Q1. If you are against loops, though, you will have answered B.

Question 9

Because we are not allowing loops, it looks at the start as if there might only be two graphs on two vertices. But then look at Figure A4 below. Are these graphs the same or different?

Figure A4: Graphs with different looking lines

Question 10

After some thought I'd guess that there are two schools of thought. Those who like C and those who like D. The problem again is 'when are two graphs the same?'. We will go for C, but why?

Question 11

There are 11 graphs on 4 vertices. We show them in Figure A5. But we show them systematically there. What system did we use? Why is the sixth one 'alone' with no partners?

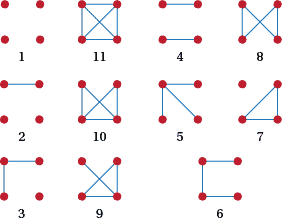
Figure A5: The simple graphs on four vertice

Question 12

Another way to do this is: is $a \leftrightarrow v, b \leftrightarrow u, c \leftrightarrow w$, and $d \leftrightarrow x$. This sends the edges $ab \leftrightarrow vu = uv, ac \leftrightarrow vw, bd \leftrightarrow ux$.

Question 13

Doing this simply, interchange the positions of $c$ and $d$ in Figure A6 and then rotate the graph .

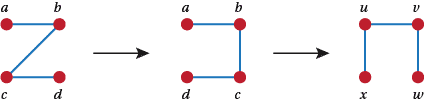
Figure A6: An isomorphic pair of graphs - from Z to $\Pi$

Using a bijection we have $a \leftrightarrow x, b \leftrightarrow u, c \leftrightarrow v$, and $d \leftrightarrow w$.

Question 14

One way to think about this is to see that there is a triangle in $G$, but not in $H$, and there is a square in $H$ but not in $G$. But $G$ and $H$ are also not isomorphic because they have different numbers of edges. Let $E(G) $ be the number of edges of $G$. Then it's easy to see that $|E(G)|= 4$ and $|E(H)| = 5$. These two reasons should be enough to settle things. However, we can look at this in another way. Look at the number of edges that go into the different vertices. Starting at the bottom right and moving around clockwise these `edge-in' numbers are for $G - 1, 2, 3, 2$ and for $H - 3, 2, 3, 2$. Surely these sequences would have to be the same if we had $G \cong H! $. So we have some tests for isomorphism.

Question 15

In order these are $(0, 0, 0, 0)$, no edges; $(3, 3, 3, 3)$, 6 edges; $(1, 1, 1, 1)$, 2 edges; $(2, 2, 2, 2)$, 4 edges; $(1, 1, 0, 0)$, 1 edge; $(2, 2, 3, 3)$, 5 edges; $(3, 1, 1, 1)$, 3 edges; $(0, 2, 2, 2$), 3 edges;$ (2, 1, 1, 0)$, 2 edges; $(1, 2, 2, 3$), 4 edges; $(2, 1, 2, 1)$, 3 edges. Make a conjecture about the relation between the degrees of a graph and its number of edges? Does that work for any graph? How would you prove it?

Question 16

There doesn't seem to be a way to get $1, 1, 1, 1, 1$. Why do you think that this is? However, the graph in Figure A7 has the sequence of degrees: 1, 1, 1, 1, 1, 1.

Figure A7: The graph with degree sequence 1, 1, 1, 1, 1, 1

Question 17

Experiment with this. What conjectures (guesses) do you have? Can you prove them? Does the Theorem (see after Q22.) help in any way?

Question 18

You can see from the simple graphs we have listed for $n = 3$ and $n = 4$ that it is possible for graphs to have every vertex of degree 0 or even just a few vertices of degree 0. But no vertex in a simple graph can have degree $n$ because there are only $n - 1$ other vertices for a specific vertex to be joined to. This is not true for graphs that are not simple though. Find an example.

Question 19

Every vertex can have degree 0 (just five vertices and no edges); every vertex can have degree 2 (we'll see later that this is called the cycle $C_5$); every vertex can have degree 4 (put in all possible edges to get $K_5$ see Q25); but there are no graphs on 5 vertices where every vertex has degree 1 or 3 (why?).

Question 20

The one with each vertex joined to all of the other vertices. The degree of each vertex is $n - 1$. The number of edges is $\frac{n(n - 1)}{2}$ (why?). Make sure that you can prove that result in 2 ways. Why isn't it $n(n - 1)$?

Question 21

No. There seem to be three non-isomorphic simple graphs with every vertex of degree 2. We've listed them in Figure A8.

Figure A8: Three non-isomorphic simple graphs with the same degree sequence

Question 22

Yes. Look at the graphs of Q11.

Question 23

Does this have anything to do with the number of edges? Does it have anything to do with the degrees of vertices? Does Q16 have anything to do with this? All of these things help to simplify things, but in the last resort you have to go back to the definition to be sure if two graphs are isomorphic.How about the number of edges or the structure of the graphs?

Question 24

This is a repeat of Q.20. For 3 vertices the maximum number of edges is 3; for 4 it is 6; for 5 it is 10 and for 6 it is 15. For $n, N = n(n - 1)/2$. There are two ways at least to prove this. We'll show you one way and then you find the another. To prove this result note that the first vertex has $n - 1$ edges coming into it. The second vertex has $n - 2$ edges that are different from the $n - 1$ going to the first vertex. The third vertex has $n -3$ new edges. This continues until the last vertex has no new edges. So the total number of edges is $0 + 1 + 2 + 3 + \dots + (n - 3) + (n - 2) + (n - 1)$. This is an Arithmetic Progression whose sum is $n(n - 1)/2$.

Question 25

The graphs required are shown in Figure A9.

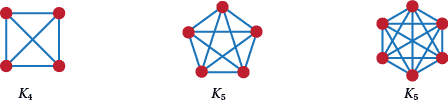
Figure A9: Some complete graphs

Question 26

For any graph with $e$ edges there is a unique graph with $N - e$ edges. Just take away all of the $e$ edges and add in all the edges that were not there in the first place. As a result if you put these two graphs on top of each other you would get $ K_n$. So we have a one-to-one link here.

Question 27

34. And this will be easier if you use Q26. Or did you use it without knowing? Also refer forward to Q38.

Question 28

We have put the two complementary pairs together in Figure A10.

Figure A10: The complementary graphs on three vertices

Question 29

If you use the definition of the complement twice on G you get back to G again.

Question 30

There is only one way for the definition to work.

Question 31

$P$ is regular of degree 6. It has 30 edges.

Question 32

These are just the complements of the graphs in the answer to Q21.

Question 33

Suppose that $G$ is a regular graph of degree $r$. Then in the complement of $G$, every vertex has degree $n - 1 - r$. So the complement is regular.

Question 34

We'll list all of the graphs with 0, 1, 2, 3, and 4 edges. The graphs on 10, 9, 8, 7 and 6 edges follow by complementation. We'll then list all of the graphs with 5 edges (some of which are self-complementary.) This is done in Figure A11.

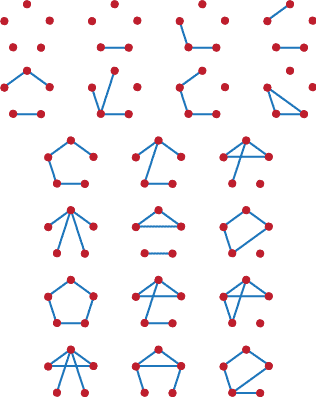
Figure A11: All the graphs on five vertices with less than or equal to five edges

Question 35

On 5 vertices: there are two of them; one with every vertex of degree 2 and the other with degrees of 1, 1, 2, 3, 3. On 6 vertices: there are none. Why not? Investigation: Let $n$ be the number of vertices of a graph. What value must $n$ have to possibly support a self-complementary graph? Can you show that for each of these values of $n$ there is at least one self-complementary graph? If so you will have proved a conjecture that says There is a self-complementary graph on $n$ vertices if and only if $n =$ whatever. This problem is a non-trivial exercise. Work on graphs on up to 13 vertices and see if you can generalise from there. You might find the graph in Figure A12 useful.

Figure A12: A graph on eight vertices

Question 36

The simple graph on 1 vertex is regular of degree 0. The graphs on 2 vertices are either regular of degree 0 or regular of degree 1. On 3 vertices there is one regular graph of degree 0 and one of degree 2. On 4 vertices there is one regular graph of degree 0, one of degree 1, one of degree 2, and one of degree 3.

Question 37

A graph with $n$ vertices and no edges is regular of degree zero. Actually it is the complement of $K_n$. For $n = 2m$, the graph consists of $m$ edges whose vertices are all distinct. For $n = 2m + 1$ no graph is possible.

Question 38

We have shown the regular graphs of degree 2 on 8 vertices in Q21; there are no others. There are no graphs that are regular of degree 3 on 9 vertices. Why? (How many edges would such a graph have?)

Question 39

There are no regular graphs of odd degree on $2n + 1$ vertices. Suppose there were. Let the odd degree be $2k + 1$. By Theorem 1, the number of edges is $(2n + 1)(2k + 1)/2$. But this is not a whole number.

Can we go further than this? What can be said about the number of vertices of odd degree in any graph? We'll prove the general result here.

Corollary

The number of vertices of odd degree in a graph is even.

Proof

By the theorem, the sum of the degrees of all of the vertices is even. But this sum is also the sum of the even degree vertices and the sum of the odd degree ones. Now the sum of the even degree vertices is even. So the sum of the odd degrees has to be even too. This means that there have to be an even number of vertices of odd degree.

$\Box$

Question 40

On 3 vertices the graphs with 2 or 3 edges will do the trick. On 4 vertices graphs 5, 6, 8, 9, 10, 11 in the answer to Q11. On the 5 vertices graphs show in Figure A12, the 9th, 10th, 12th, 15th, 16th, 18th, 19th and 20th in the answer to Q38. The complements of some of the graphs there are also connected. Which ones?

Question 41

There are several of these. We give three in Figure A13, but you might try to find them all. Be systematic!

Figure A13: Some connected graphs on 6 vertices with 6 edges

Question 42

On 3 vertices: the graphs with none and one edge. On 4 vertices: from Q 11, these are graphs 1, 2, 3, 4, and 7.

Question 43

Connected graph: take $K_{n-1}$ and add a vertex to get a connected graph. Disconnected graph: the vertex of degree $n - 2$ is joined to $n - 2$ vertices. There is still a vertex not joined to any other vertex, so this graph is disconnected.

Question 44

Never. Suppose that $G$ is disconnected, then there exists a vertex $u$ that is not joined to at least one other vertex. If $u$ is not joined to any other vertex, then$ u$ is joined to every vertex in its complement. Suppose that $v$ is adjacent to $u$ in $G$. Let $U$ be the set of vertices not connected to u directly or through other vertices of $G$. By definition $v$ is not adjacent to a vertex in $U$. Let $V$ be all the vertices adjacent to $u$ in $G$. Then in $\tilde{G},$$u$ is joined to every vertex in $U$ and so is every vertex of $V$. Hence $\tilde{G},$ is connected. (If you don't see how this works, try the idea out on some specific disconnected graphs.) In general, at least one of a graph or its complement is connected. This follows from the argument above. All the graphs in Figure A13 have a connected complement. So a graph and its complement can both be connected.

Question 45

Just $K_n$ because it is clearly connected and has the most edges of any graph on n vertices. Can you do better than $K_{n-1}$ plus an extra vertex of degree 0? Why? Why not?

Question 46

On 3 vertices: 1 graph with 2 edges; on 4 vertices: 2 graphs with 3 edges; on 5 vertices: 3 graphs with 4 edges. You can find them easily from the graphs in Q11 and Q38.

Question 47

Conjecture 1

The fewest edges a connected graph on $n$ vertices has is $n - 1$.

1. No graph with $n - 2$ edges is connected.
2. Not all graphs with $n - 1$ edges are connected.
3. Not all graphs with $n$ edges are connected.

Your proof has to take into account all the notes above. We'll give a proof of all the conjectures later in the text.

Conjecture 2

The number of connected graphs on n vertices is $n- 2$.

Conjecture 3

In some graphs there is only one way to go from one given vertex to another given vertex.

Conjecture 4

Suppose we have a connected graph. If there is only one way to get from any vertex to any other then the graph has no cycles.

Check your conjectures out on graphs with 6 vertices to see if they are still true.

Question 48

You will have done all sorts of trees. In Figure A14 we give just three.

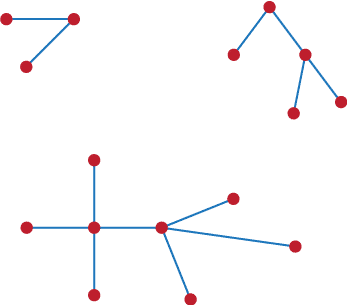
Figure A14: A random three trees

Question 49

There is no formula for the number of trees on n vertices — see https://en.wikipedia.org/wiki/Tree_(graph_theory).

Question 50

This can be done for all connected graphs, but you have to be careful to take off edges that don't disconnect the graph. How do you know when to stop though?

Question 51

It looks as if they all have at least two vertices of degree 1. Are there some trees with only 2 vertices of degree 1? But how to prove these things? We'll take this up in the text later when we prove a series of results about trees.

Question 52

There are a lot of them (11). In fact all of the graphs on 4 vertices (see Q11) are subgraphs of $K_4$.

Question 53

From Q11, with two components: 3, 4, 7; and with three components: 2.

Question 54

It is $K_n$.

Question 55

Conjecture: They are connected. Proof: Since trees are connected, then so must be a graph with a tree as a subgraph. (Also: if the graph has $n$ vertices it has to have at least $n - 1$ edges.)

Question 56

They are connected, so they can't have degree 0 or 1; there is no spanning graph of degree 2 (see Q88); so every regular spanning graph of $P$ is $P$.

Question 57

The answers are shown in Figure A15.

Figure A15: Some of the small cycles

Question 58

All the cycles from $C_3$ up to $C_n$.

Question 59

There are no cycles in any tree. Suppose there were. Then you could delete an edge from that tree and it would still be connected. But this would contradict the condition of trees having the minimum number of edges in any connected graph on a given number of vertices.

Question 60

Is the connected graph $G$ in Figure A16 the only one possible?

Figure A16: The required graphs G and H

The graph $H$ in Figure A16 has the required property. (It also has a $C_3$ and a $C_4$.)

Question 61

In P, you can find $C_5$ (on the vertices 1, 2, 3, 4, 5, for example), $C_6$ (2, 3, 4, 5, 10, 7), C8 (6, 8, 3, 2, 1, 5, 4, 9), and C9 (2, 3, 4, 5, 10, 8, 6, 9, 7), but no other cycles. In $\tilde{P}$ you can find lots of cycles of every type from $C_3$ up to $ C_10$.

Question 62

The conjecture is false for $n = 3$ and 4. Conjecture: For $n > 4$, $\tilde{C_n}$ is connected. Proof Number the vertices from 1 to $n$ in order around the original cycle. $\tilde{C_n }$ contains tree with edges 1 to $i$ for all $i \ne 2$ or $n - 1$, and 4 adjacent to 2 and $n - 1$.

Question 63

We'll illustrate this in Figure A17 using $i = 3$ and $n = 6$. The original $P_3$ has red edges; the remainder of the tree has dotted edges. There are clearly many more trees that have $P_3$ as a subgraph. In general start with the given $P_i$ and add edges until a tree on $n$ vertices is formed.

Figure A17: A tree on six vertices containing the subgraph $P_3$

The answer to the uniqueness is 'sometimes'. For instance, there is only one tree on 4 vertices with $P_3$ as a subgraph. What do you think of the following conjecture?

Conjecture

Let $n > 4$. Suppose that we have a tree with $P_i$ as a subgraph then the tree is unique if and only if $ i = n$.

Question 64

Yes. Just delete an edge of the cycle. No. For example, any complete graph has a spanning path.

Question 65

Yes. If a graph has a spanning path, then it is possible to go from any vertex to any other vertex by edges of the graph. Hence the graph is connected. No. The graphs in Figure A14 (the answer to Q48) are connected graphs that don't have spanning paths.

Question 66

In Figure 4, the path 1, 2, 3, 4, 5, 10, 8, 6, 9, 7 is one possible spanning path. How many more are there? (See also Q106.)

Question 67

Yes, there are lots of them.

Question 68

Yes, again there are generally lots of them. The thing that distinguishes connected graphs from disconnected graphs is that connected graphs have spanning trees. So we'll conjecture that a graph is connected if and only if it contains a spanning tree.

Question 69

Two! Yes. Why?

Question 70

$n$, because every vertex is joined to every other vertex.

Question 71

2, just alternate the colours as you go from one end of the path to the other.

Question 72

2 if $n$ is even and 3 if $n$ is odd.

Question 73

First it can't take just 2 colours because P contains a $C_5$. We can colour it with 3 colours though. One way to do this it to colour the vertices 1, 4, 7, 8 with colour A; 2, 5, 6 with colour B; and 3, 9, 10 with colour C.

Question 74

Our original definition assumes that trees are connected and Theorem T1 shows that they are acyclic. If a graph is connected and acyclic we only have to prove that it has the fewest edges of any connected graph to show that it is a tree in our original definition. If the graph is acyclic, then the proof of the Corollary to Theorem T1 still holds and shows that there is a unique path between any two vertices. Hence if we remove an edge, some vertices will no longer be joined. So an acyclic connected graph has the fewest edges of all connected graphs.

Question 75

Can you tell by looking at the sorts of cycles they have?

Question 76

The only such graphs are $\tilde{K_n }$. This is because no vertex is adjacent to any other vertex so they only need one colour.

Question 77

Any odd cycle will do.

Question 78

Figure A18: The bipartite graphs with most edges on 3, 4 and 5 vertices.

Question 79

Let the vertices of a bipartite graph be coloured in two colours, red and blue. By the definition of colouring, red vertices are only adjacent to blue vertices and vice versa. Let the red vertex set be $X$ and the blue vertex set be $Y$. Then this satisfies the $X, Y$ definition of bipartite.

Starting with the$ X, Y$ definition let the vertices of $X$ be coloured red and the vertices of $Y$ blue. This gives us the 2 colouring definition.

Question 80

The graphs are shown in Figure A19

Figure A19: Three particular complete bipartite graphs.

Question 81

The disjoint union of $K_m$ and $K_n$ (a copy of $K_m$ together with a copy of $K_n$).

Question 82

$ mn$ because every vertex in the $m$ set has degree $n$.

Question 83

In order these are 4; 4; 4; 4 and 6; 4 and 6; none; 4, 6 and 8.

Question 84

$2, 4, 6, \dots, 2m$.

Question 85

Conjecture

A graph B is bipartite if and only if it has no odd cycles. The proof is not straightforward. It is to be found in the next section of the text as is the answer to the tree's question.

Question 85

$K_n$ is planar for $n \le 4$ and non-planar otherwise. You may think that $K_4$ is non planar but it can be drawn as in Figure A18 where no edges cross. To prove that $K_5$ is non-planar requires the use of the Jordan Curve Theorem. You might want to look this up but it is beyond the scope of this course.

Question 86

$K_{m,n}$ is planar for $2 \le m \le n$ and non-planar otherwise. Figure A18 shows a non-planar drawing of $K_{2,3}$. Again to show that all of the other complete bipartite graphs are non-planar requires the Jordan Curve Theorem.

For regular graphs there is no order. True all regular of degree 2 graphs are planar but from there on some are and some aren't. For example, it is easy to draw a planar graph on 10 vertices that is regular of degree 3, but $P$ is regular of degree 3 on 10 vertices and is not planar.

Self-complementary graphs are non-planar as soon as they get to have more than 8 vertices.

Trees and cycles are always planar.

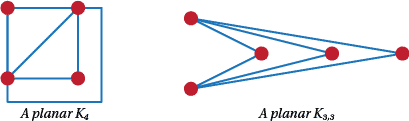
Figure A20: Some examples of planar graphs.

Question 87

If $K_5$ is non-planar, then so is $K_n$ for $n > 5$, because $K_5$ is a subgraph of all of these. The same argument shows that if $K_{3,3}$ is non-planar so are $K_{m,n}$ for $3\le m \le n$.

We show a `sort of' $K_{3,3}$ in $P$ in Figure A21. The blue lines represent the edges of the $K_{3,3}$ and the red and green vertices are the two sets of vertices.

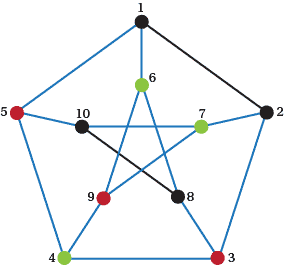
Figure A21: A $K_3$ in $P$.

We show some of the graphs in Table A1.

Table A1: A table to see any patterns in numbers of vertices, edges and faces

Graph	Vertices	Edges	Faces
A tree on $n$ vertices	$n$	$n-1$	$1$
$C_n$	$n$	$n$	$2$
$K_4$	$4$	$6$	$4$
$K_2$	$n+2$	$2n$	$n$

Do you see any patterns in these numbers? Do they hold for every planar graph you can think of?

Question 90

The proofs that you will find assume that the graph being dealt with is connected and planar.

Now, why do we need connected? Can you find a disconnected planar graph that doesn't satisfy Euler's formula?

Does it make sense to think about faces for non-planar graphs?

Question 91

By the results in the tree section these can only be trees; Trees with one edge added (so they have one cycle). They are connected so they must have spanning trees. But we need to add one more edge. (iii), (iv), and (v) are shown in Figure A22.

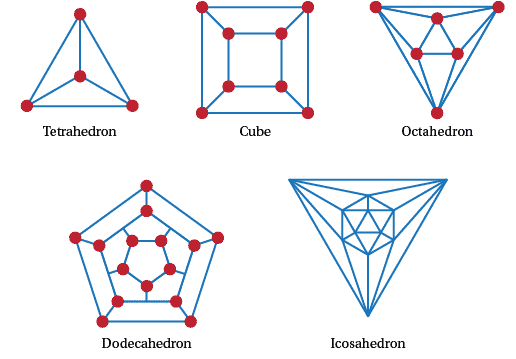
Figure A22: The graphs of the Platonic solids.

(see https://www.bing.com/images/search?q=graphs+of+the+platonic+solids&qpvt=graphs+of+the+platonic+solids&FORM=IGREa)

Question 92

We'll do this for the graphs that have degree 3 and leave the others to you. Since $2e$ is the sum of the degrees, suppose we have $n$ vertices then $2e = 3n$. If every face has $r$ vertices, then $rf$ counts each vertex 3 times and so $3n = rf$. Put these numbers into the Euler formula and we get $n - 3n/2 + 3n/r = 2$. Rearranging we get $4 = 6n/(n + 4)$. To make life easier for ourselves rearrange to get $r = 6 - 24/(n + 4)$. So $n + 4$ divides 24 to give $n = 4, 8$ and $20$ (no graphs exist for lower divisors of 24). Hence we get the right numbers for the Platonic graphs of degree 3. We omit showing that there is only one graph for each of these three sets of vertices, edges and faces.

Question 93

Look both of these up on the web and compare them. Take a face of one of the solids and make it the outer face of the graph. Then squash `project' the solid onto the plane.

Question 94

Put a vertex in a face of a Platonic graph and join two vertices if they are in adjacent faces. What graphs do you get? What does the tetrahedron's new graph look like? How about the cube or the dodecahedron?

Question 95

It is easy to find a disconnected planar graph for which Euler's Polyhedral Formula doesn't hold.

For a formula for disconnected graphs see https://en.wikipedia.org/wiki/Euler_characteristicSurfaces.

Question 96

See https://en.wikipedia.org/wiki/Euler_characteristicSurfaces.

Question 97

There are lots of possibilities here, actually an infinite number because you can keep repeating any edge you like. So long as you go vertex, edge, vertex, etc. and the edge between two vertices joins the two vertices you have a walk.

Question 98

You might want to make sure that every edge of a walk appears only once - if you want to make sure that you go over every 'bridge' once and only once. You might want to make sure that every vertex of a walk appears only once - if you want to make sure that you get to each 'land mass' once and only once. You might want to make sure that the first and last vertex of a walk is the same - if you want to make sure that you get back to where you started. You might want to make sure that the first and last vertex of a walk are different - if you want to make sure that you don't get back to where you started.

Question 99

Complete graphs have Euler tours if and only if they have every vertex even. This means that the number of vertices is odd. So $K_n$ has an Euler tour if and only if $n$ is odd. You can only get an Euler trail if $n = 2$.

Complete bipartite graphs $K_{m,n}$ have Euler tours if and only if $m$ and $n$ are both even. On the other hand they have an Euler trail if and only if $m = 2$ and $n$ is odd.

Platonic graphs are shown in Figure A22. Only one, the octahedron, has an Euler tour because it is the only one that is regular with an even degree. None of them have Euler trails.

The Petersen graph can't have either a tour or a trail because every vertex of $P$ is odd (three). Clearly this applies to every regular graph of odd degree. On the other hand regular graphs with even degree al have Euler tours.

Question 100

Disconnected graphs don't have edges from one component to another. Hence no Euler tour or Euler trail.

Question 101

Add an edge between the two vertices of odd degree. (This may give you a multigraph but that is OK because the Euler Theorems apply to multigraphs.) This new graph has an Euler tour because every vertex has even degree. Now remove the added edge and the Euler tour we have just found becomes an Euler trail.

Question 102

What if a delivery van needs to drop something at every house in every street of a suburb? It would be good to know if the street graph has an Euler tour as then the van's work can be done efficiently. Even an Euler trail would make life easier.

Question 103

See https://en.wikipedia.org/wiki/Icosian_game.

Question 104

All complete graphs on $n$ vertices have spanning cycles because they have all graphs on $n$ vertices as spanning graphs. Likewise they all have Hamiltonian paths.

Question 105

$K_3$ has one Hamiltonian cycle; $K_4$ has one Hamiltonian cycle and two non-adjacent edges left; $K_5$ has two disjoint Hamiltonian cycles; and $K_6$ has two Hamiltonian cycles and three non-adjacent edges left over.

If you try to generalise this you might conjecture that (i) for $n$ is odd $K_n$ has $(n - 1)/2$ edge disjoint Hamiltonian; and (ii) for $n$ even $K_n$ has $(n- 2)/2$ edge disjoint Hamiltonian cycles and $n/2$ independent edges. Are these conjectures true?

Question 106

$P$ has no Hamiltonian cycle.

Suppose then that it does have a Hamiltonian cycle. Therefore it has to use an even number of the edges 16, 27, 38, 49, 5 10, which we'll call the cross edges.

1. Without loss of generality assume that it uses four of these edges and the cross edge not used is 16. Colour the not used edge in blue as in Figure A20. This means that it must use the red edges in Figure A20. But the red edges form a cycle that is not a Hamiltonian cycle. So Step 1 can't apply.

   

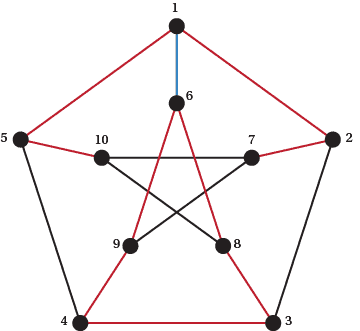
   Figure A23: $P$ is not Hamiltonian, Step 1.

2. Assume that only two of the cross edges are used. Without loss of generality we can assume that (a) 16 and 5 10 are used or that (b) 16 and 38 are used. If 16 and 5 10 are used, then 27, 38 and 49 are not used so we colour these in blue (see Figure A21). The red lines that have to be in the Hamiltonian cycle so far are coloured red. But there is already a cycle here so there can't be a Hamiltonian cycle.

   

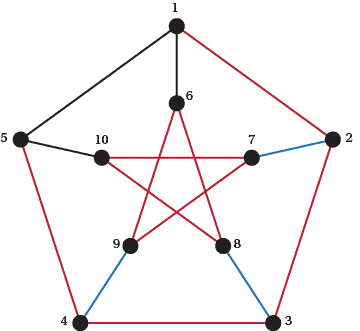
   Figure A24: $P$ is not Hamiltonian, Step 2a.

Assume that 16 and 38 are used. This also leads to a contradiction, but we leave that for you to complete.

3, 8, 6, 1,2,7, 10, 5, 4, 9 is one of many Hamiltonian paths in $P$.

Question 107

Unfortunately there is no nice characterisation for Hamiltonian cycles like the Euler Tour Theorem. In fact even finding a Hamiltonian cycle in a given graph is NP complete (which means it's pretty hard to do!). There are some valuable results but they are not easy to state. Search the web to see what results are known.

Question 108

Draw a $5 \times 5$ board and put a vertex in the centre of each square. Then join two vertices if it is possible for a Knight to move between the corresponding squares. Show that this graph has a Hamiltonian cycle.

Question 109

The answer can be found at https://en.wikipedia.org/wiki/Knight's_tour.

Question 110

The adjacency matrix of a complete graph consists of ones except for the main diagonal which is all zeros.

For a bipartite graph with parts of size $m$ and $n$, there is an $m \times m$ block of zeros in the top left hand corner of the adjacency matrix and an $n \times n$ block in the bottom right hand block. The other blocks are $m \times n$ and $n \times m$ and each is the transpose of the other.

Question 111

Replace all 1s by zeros and all zeros, except the ones on the main diagonal, by 1s.

Question 112

An adjacency matrix has to have the following properties:

• It is symmetric;
• Its entries are from the set $\{0, 1\}$; and
• The main diagonal consists only of zeros.

Show that these are necessary and sufficient conditions for a matrix to be an adjacency matrix or find all the necessary and sufficient conditions.

Question 113

The sum of an adjacency matrix with itself has a 2 when the graph has an edge and a zero otherwise. The square of an adjacency matrix tells you something about the number of walks of length two. What is that?

we can see that the entries have something to do with walks. It turns out that in general the $i, j$ entry in the matrix $A^k$, tells you how many walks of length $k$ there are from vertex $i$ to vertex $j$.

Question 114

The answer is 6.

Question 115

Think of the 9 people as vertices of a graph and join those who know each other. Let $u$ be adjacent to $u_i$ for $i = 1, 2, 3, 4, 5, 6$. If $v$ and $w$ are the remaining vertices we know that one of $u_i$ has degree at least five. Hence $u_i$ knows $u_j$ for some $j$ and we have our triangle.

Question 116

The steps here are to note (i) that two people must have shaken hands the same number of times, so one of these is the male host; (ii) one person has to have shaken hands 8 times. Now remove the two people who have shaken hands the same number of times. Repeat everything above to reduce the number of people under consideration to 4 and so on. On a countback you'll see that the man and his wife had shaken hands with 4 people.

Question 117

Trying a few small cases shows that if $n = 1$, the answer is 1; $n = 2$ gives 2 (include the labelled graph with no edges); $n = 3$ gives 8; and higher values of $n$ give powers of 2 as well. But what is the power here? It's the number of possible edges. To show this note that every edge is used or not used. So the number of edges is $2^{n(n-1)/2}$.

Question 118

Three times. The edges of $K_6$ can be divided into 3 Hamiltonian paths.

Question 119

This is a graph on 20 vertices whose edge set is a union of edges. So the degrees of all of the vertices are less than 3 and the graph is a disjoint union of even cycles. It is then possible to get an independent set of size 10.