Content
Circuits
In the Walking Problem at the start of this graph business, we looked at trying to find how to get across different bridges and get back to the start again. Figure 5 below is derived from Figure A1 in the answers. If the gentry followed $A e_1 B e_2 A e_5 C e_4 B e_6 D e_3 B$ they would have missed $e7$, but they would have certainly been on a walk. Probably for reasons similar to this, we define a walk on a (not necessarily simple) graph to be a sequence of vertices and edges, where, of course the edge between two given vertices in the walk actually joins these two vertices.
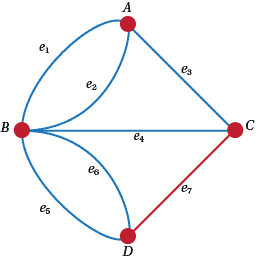
Figure 12: A labelled graph of the Königsberg problem
Questions
- Find other walks on the graph of Figure 5.
- Now there are all sorts of variations on this general definition where we make some sort of restriction. See if you can think of at least three variations on this theme. In what circumstances might these definitions be useful?
So Euler was interested in walks where every edge of the graph was used and the initial and final vertices were the same. He had no luck there. So he simplified things a bit to asking for a walk that used every edge but the first and last vertices were different. He failed there too. If he had been Hamilton, he would have looked for walks that went through every vertex once and only once whether or not the first and last vertex were the same. Now we know that Euler managed to settle The Walking Problem in general, and you know that we've pretty well solved this, but let's put it in formal words.
So let's define an Euler trail to be a walk in which every edge occurs exactly once and where the first and last vertices are different. On the other hand we'll call an Euler tour a walk in which every edge occurs exactly once and where the first and last vertices are the same. Let's think about this in the context of The Walking Problem. What the citizens of Königsberg really wanted was to find an Euler tour around their bridges. They might even have settled for an Euler trail. Euler resolved both these issues when he found the next two Theorems.
Theorem (Euler's Tour Theorem)
A connected graph has an Euler tour if and only if the degree of every vertex is even.
The proof of this is too long and involved for this pulication but it can be found in many places. You might try Clark and Holton, A First Look at Graph Theory, World Scientific, 1996 or some other graph theory text book.
Theorem (Euler's Trail Theorem)
A connected graph has an Euler trail if and only if it has two vertices of odd degree and the rest of even degree.
Note that both of these last two theorems apply equally to simple graphs and multigraphs.
Questions
- Which complete graphs have Euler tours and which have Euler trails? Repeat with complete bipartite graphs and the Platonic graphs. How about $P$?
- Why do the two theorems above only talk about connected graphs?
- Prove the Euler Trail Theorem assuming that the Euler Tour Theorem is true.
- Do these theorems have any practical uses?
Euler's activity occurred in 1736. It took another 100 years or so before William Rowan Hamilton thought that it might be interesting to look at graphs that had a walk that went through every edge once and only once. So consider a Hamiltonian cycle to be a cycle that goes through every vertex of a graph. Similarly we define a Hamiltonian path. Incidentally Hamilton got his name attached to these objects because in 1857 he invented a game. His Icosahedron Game Game requires the player to find a Hamiltonian cycle around a dodecahedron. See https://en.wikipedia.org/wiki/Icosian_game
Questions
- Show that a dodecahedron has a Hamiltonian cycle.
- Investigate complete graphs to see which of them have Hamiltonian cycles and which have Hamiltonian paths.
- How many disjoint Hamiltonian cycles does a complete graph have? That is, how many Hamiltonian cycles do they have that have no vertices in common?
- Does $P$ have a Hamiltonian cycle or path?
- Investigate graphs with and without Hamiltonian cycles to see if you can find some nice theorems.
- A Knight's tour (see https://en.wikipedia.org/wiki/Knight's_tour) is a series of moves that takes a Knight around a chessboard from a given square visiting each square once and only once and returning to the original square. (In other words it's a Hamiltonian cycle on a particular graph defined by the moves of a Knight.) Show that such a tour exists on a $5 \times 5$ board.
- For what $m$ and $n$ are Knight's tours possible on an $m \times n$ board?
As well as Euler, Hamilton has a famous connection with bridges. It was actually a piece of vandalism. He had been working on a problem for a long while and one day he went with his wife on a walk by a river, or maybe a canal, I'm not sure. Suddenly, near a bridge, out of the blue he solved his problem. He had invented quaternions. He was so excited that he carved the basic equations on the bridge!
