Content
Planarity
Go back to Q7 for a moment. In that problem we wanted to know if it was possible to make some connections between three services and three houses so that the connections didn't cross. This produces a graph which is bipartite. Actually it is $K_{3,3}$. From what we saw there, we can't draw that graph in the plane so that none of its edges cross. However, many graphs can be drawn this way. For example, all trees and cycles. We call them planar. So a graph is planar if we can find some way to draw it in the plane so that no two edges cross.
Let's underline this. If a graph can be drawn in the plane so that no two edges cross it is planar. On the other hand, non-planar graphs can never ever be drawn in the plane without some edges crossing. However, it may be possible for a planar graph to be drawn with crossed edges, but it doesn't make it non-planar. We underline this in Figure 11. $K_4$ is first drawn with a crossing, and then without any crossings. So $K_4$ is planar. On the other, no matter how hard you try you will never be able to draw $K_5$ without a crossing.
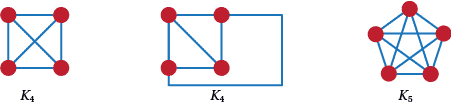
Figure 11: some drawings of planar and non-planar graphs
Questions
- Now look back at all the graphs you have met so far. Which of them are planar? Particularly look at all the graphs on up to 5 vertices; complete graphs; complete bipartite graphs; regular graphs; self-complementary graphs; trees; and cycles. Make and prove conjectures, or find counter examples to, about all of these.
- Show that $K_n$ is non-planar for all $n \ge 5$. For what $m$ and $n$ is $K_{m,n}$ non-planar?
- This last question leads to a characterisation of planarity by Kuratowski. See https://en.wikipedia.org/wiki/Kuratowski's_theorem
but we have to be a bit loose in the statement we are going to make. A graph is non-planar if and only if it contains a $K_5$ or a $K_{3,3}$. Can you use this statement to show that $P$ is non-planar?
Look up Kuratowski's Theorem to see precisely what it says.
Questions
- If a planar graph is drawn so that no edges cross, it will not only have vertices and edges, it will also have faces. These are regions in the plane whose points can be joined by lines that do not cross an edge or meet a vertex of the graph. As such there is always one face 'outside' or 'around' the graph. Draw up a table for the numbers of vertices, edges and faces for all of the connected planar graphs in Q86. Is there a pattern?
- One of the basic results of planar graph theory is Euler's Polyhedral Formula. Look this up on the web. Find a proof of it. Is this formula a necessary and sufficient condition for a connected graph to be planar? That means the two implications 'If a connected graph is planar then it satisfies the Euler Formula' and 'if a connected graph satisfies the Euler Formula then it is planar'.
- Find all connected planar graphs with the following properties:
- The number of vertices is one more than the number of edges;
- The number of vertices is the same as the number of edges;
- All the faces have the same number of vertices and all the vertices have degree 3;
- All the faces have the same number of vertices and all the vertices have degree 4;
- All the faces have the same number of vertices and all the vertices have degree 5.
Questions
- The graphs of Q91 dotpoint 3, dotpoint 4 and dotpoint 5 are called the Platonic graphs. These graphs have the property that they are all regular and all of the faces have the same number of vertices. Show that they are the only Platonic graphs.
- How are the Platonic graphs related to the Platonic Solids?
- How are the Platonic graphs related to the Platonic graphs? (Are they linked in some way? Try putting a vertex in a face. How might two vertices be joined?)
- We have been careful to use the word `connected' when talking about Euler's Formula. Why?
Can we get a formula for disconnected graphs?
Questions
- Just in case you are not sure by now, Euler's Polyhedral Formula is $v - e + f = 2$, where $v$ is the number of vertices, $e$ the number of edges and $f$ the number of faces. Call a graph toroidal if you can draw it on a torus (doughnut with a hole) so that no two edges cross. Does Euler have anything to say about these graphs in terms of $v, e$ and$ f$?
