Content
Trees
Now Question 40 introduces the concept of connectivity in graphs. A graph is connected if it is possible to move from any vertex of the graph to any other vertex using edges of the graph.
Questions
- Draw two non-isomorphic connected graphs on 6 vertices that have 6 edges.
- A graph that is not connected is called disconnected. Find all of the disconnected graphs on 3 and 4 vertices.
- Is it possible for a connected graph on n vertices to have a vertex of degree $n - 2$? Is it possible for a disconnected graph on $n$ vertices to have a vertex of degree $n - 2$?
- When is the complement of a disconnected graph disconnected? Is the following true or false? At least one of a graph or its complement is connected. If it is true prove it; if it is false provide a counterexample. Is it possible for a graph and its complement to both be connected?
Mathematicians often look at extremes to see what it tells them. As far as connectivity is concerned one sort of extremeness is about the number of edges. So let's look at the extremes of connectivity.
Questions
- What connected graphs on $n$ vertices have the most edges?
- What connected graphs on 3, 4 and 5 vertices have the least number of edges?
- On the basis of the last question what is the least number of edges a connected graph on $n$ vertices has? Can you state this carefully as a conjecture? Can you prove your conjecture? Can you think of any other conjectures about connected graphs? Can you prove them?
The connected graphs that have the smallest number of edges seem to look a bit like trees. You could draw them all as having a root or roots and having branches. So we'll make a definition.
Definition
A graph on $n$ vertices is called a tree if it is connected and has the fewest number of edges among all connected graphs on n vertices.
Questions
- Draw some trees.
- How many trees do you think there are on $n$ vertices?
- Remove some edges from a graph so that a tree is left. Can this be done for all graphs?
- How many vertices of degree 1 have to exist in a tree on 2 or more vertices?
Subgraphs
This seems a good point to talk about subgraphs.
Let $VH$ denote the set of vertices of graph $H$ and $VG$ the set of vertices of graph $G$.
Definition
A subgraph $H$ of a graph $G$, is any graph such that $VH$ is a subset of $VG$ and all the edges of $H$ are also edges of $G$. We also think of $G$ itself as being a subgraph of itself.
Note that you can't just say that a subgraph of $G$ consists of vertices and edges from $G$ because you have to include among the vertices of a subgraph, vertices that your chosen edges are adjacent to.
Questions
- What can be said about the subgraphs of $K_4$?
- A maximal connected subgraph of a disconnected graph $G$ is called a component of $G$. Find all of the graphs on 4 vertices that have two and three components.
- Subgraphs that have the same set of vertices as the graph they are in, are called spanning subgraphs. What can be said about a graph $G$ if it has $K_n$ as a spanning subgraph?
- What can be said about graphs that have a tree as a spanning subgraph? Make and prove a conjecture about this.
- What can be said about the regular spanning subgraphs of $P$?
Right about now it's also useful to introduce the concept of a cycle. This is just what it sounds like: a series of vertices and edges that close up.
Definition
A cycle is a connected graph of degree 2. The cycle on $n$ vertices is called $C_n$. Cycles appear as subgraphs of lots of graphs. For instance there are several subgraphs that are cycles in the graph of Figure 8.
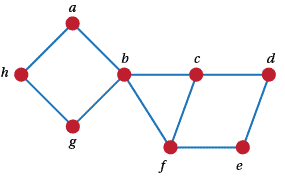
Figure 8: A graph with cycles
In Figure 8 $\{a, b, g, h\} $ defines a cycle with four edges $ab, bg, gh, ha$. In future, if we know the vertices we won't bother using the edges in saying what the cycle is.
Questions
- Draw the graphs $C_3$, $C_4$ and $C_6$. Find all other cycles in Figure 8.
- What cycles are there in $K_n$?
- What cycles are there in a tree?
- Show that there is a connected graph $G$ on 6 vertices that has 6 edges and contains a $C_5$. Does there exist a disconnected graph $H$ on 6 vertices that has 6 edges and contains a $C_5$?
- What cycles are there in $P$? What cycles are there in the complement of $P$?
- Conjecture: $\widetilde{C_n}$ is connected. If the conjecture is true, prove it. If the conjecture is false, correct it and prove that your correction is true.
Another useful kind of graph is a path.
Definition
A path is a sequence of $s$ distinct vertices and the $s - 1$ edges between them. We show the general idea in Figure 6. If a path has $n$ vertices it is denoted by $P_n$.
![]()
Figure 9: A path
As you can see a path consists of two vertices of degree 1 and a number of vertices of degree 2.
Questions
- Show that for each given value of $i$, for $i = 2, 3, 4, \dots, n$ a tree on $n$ vertices can be constructed that has $P_i$ as a subgraph. Is this tree unique?
- Is it true that a cycle has a spanning path? Is it true that a graph with a spanning path is a cycle?
- Is it true that a graph with a spanning path is connected? Is it true that every connected graph has a spanning path?
- Does $P$ have a spanning path?
Now a given connected graph may not be a tree but it can be related to a tree?
Questions
- Can you find trees in the connected graphs on 3, 4 and 5 vertices?
- Can you find trees in the disconnected graphs on 3, 4 and 5 vertices? So how can trees distinguish between connected and disconnected graphs? Can you state these ways carefully as conjectures? Can you prove your conjectures?
Colouring vertices and edges is a favourite game of graph theorists because of both the applications and the nice mathematics that it produces. Let's think for a minute of colouring vertices. We do this so that adjacent vertices have different colours and call it a vertex colouring if the colouring contains the fewest number of colours.
Questions
- Take any tree on 3, 4 or 5 vertices. Produce a vertex colouring of this tree. What is the smallest number of colours that you need? Does this work for trees on n vertices?
- How many different colours does it take to produce a vertex colouring of $K_n$?
- How many different colours does it take to produce a vertex colouring of $P_n$?
- How many different colours does it take to produce a vertex colouring of $C_n$?
- How many different colours does it take to produce a vertex colouring of $P$?
Now is the time to put together all of the results we have about trees.
Theorem (T1)
A tree on $n$ vertices has no cycles.
Proof
Suppose that a tree, $T$, has a cycle, $C$, with an edge $uv$. Since $T$ is connected there is a path $Q$ in $T$ from any vertex $a$ to any vertex $b$. Delete the edge $uv$ from $T$. If $Q$ contains the edge uv, then we can form another path $Q'$ which doesn't have $uv$ but does have other edges of $C$. Hence, since $T$ has the minimal number of edges for a connected graph, it doesn't have a cycle.
$\Box$
Corollary
In any tree there is a unique path between any two vertices.
Proof
Let $Q = xu_1u_2u_3\cdots u_ry$ and $R = xv_1v_2v_3\cdots v_sy$ be two paths in $T$ between $x$ and $y$. Moving along $Q$ from $x$, let $u$ be the last vertex that $Q$ and $R$ have in common and let $v$ be the next vertex after $u$ that $Q$ and $R$ have in common. Then there is a cycle in $T$ formed by edges of $Q$ and $R$, containing the vertices $u$ and $v$. This contradicts the theorem, so a tree has a unique path between two given vertices.
$\Box$
Questions
- Trees are usually defined as being acyclic5 connected graphs. Show that this is equivalent to the definition that we have been using. We will use the 'acyclic connected' definition from now on.
Theorem (1)
Let $T$ be a tree with at least two vertices. Let $P_r = u_1u_2u_3\cdots u_r$ be a longest path in $T$. Then $u_1$ and $u_2$ have degree 1 in $T$.
Proof
Suppose that $u_1$ has degree at least 2. Then there $u_1v$ is an edge in $T$. If $v$ is one of the vertices of $P_r$, then there is a cycle in $T$. This contradicts Theorem T1. So $vu_1u_2u_3\cdots u_r$ is a path in $T$ which is longer than $P_r$. This contradicts the assumption that $P_r$ was the longest path in $T$. Hence there is no edge $u_1v$ and degree of $u_1$ is 1. In the same way we can show that $ur$ also has degree 1.
$\Box$
Corollary
A tree on n > 1 vertices has at least two vertices of degree 1.
Proof
Such a tree has at least one edge, so it has a longest path. This longest path has two vertices of degree 1 by the theorem.
$\Box$
Theorem (2)
A tree on $n$ vertices has $n - 1$ edges6.
Proof
We will use induction on $n$.
- The tree with 1 vertex has $n - 1 = 0$ edges. So the result is true for $n = 1$.
- Assume that a tree with $k$ vertices has $k - 1$ edges.
- We will prove that a tree with $k + 1$ vertices has $k$ edges. When this is done we will have proved the theorem.
Let $T$ be a tree on $k + 1$ vertices. Let $v$ be a vertex in $T$ of degree 1. (This exists by the Corollary to Theorem T2.) Let $uv$ be the edge of $T$ adjacent to $v$. If $x$ and $y$ are two vertices of $T$ neither of which is $v$, then there is a path from $x$ to $y$ because $T$ is connected. Further this path doesn't go through $v$ because $v$ has degree 1.
Consider $T - v$, the graph obtained by removing $v$ and the edge $uv$ from $T$. We want to show that $T - v$ is a tree so that we can use Step 2. From what we have said about the path from $x$ to $y, T - v$ must be connected. $T - v$ cannot contain a cycle otherwise a cycle would already have existed in the tree $T$.
So $T - v$ is a tree and by the inductive Step 2, we Know that $T - v $ has $ k - 1$ edges. Since $T$ has one more edge that this it has the $k$ edges we were hoping for.
$\Box$
In Conjecture 2 of the answer to Q47 we suggested that there were $n - 2$ connected graphs on $n$ vertices. But generally there are more than $n - 2$ trees on $n$ vertices. We show that the conjecture is false in Figure 10 by showing five different trees on 6 vertices. You should do a quick check to make sure that these graphs are not isomorphic.

Figure 10: Five trees on 6 vertices
Theorem (3)
A graph is connected if and only if it has a spanning tree.
Proof
Clearly if a graph has a spanning tree it is connected. Suppose that $G$ is connected on $n$ vertices. If $ |E(G)| = n - 1$, then $G$ is a tree because it has the minimum number of edges possible in a connected graph. If $ |E(G)| > n - 1$, then $G$ is not a tree. So $G$ must contain a cycle. Choose any edge $e$ on a cycle of $G$ and remove it. Now $G - e$ is either a tree and so a spanning tree of $G$, or $G - e$ contains a cycle. We continue removing edges from cycles until we produce the spanning tree we are after.
$\Box$
The vertices of a tree can be coloured in two vertices so that no two vertices with the same colour are adjacent. We'll leave the result about the two colouring of the vertices of trees because that will be easier once we have a bigger result. In conclusion on trees we combine all that we have done so far in the following result.
Theorem (T4)
Let $G$ be a graph on n vertices. The following statements are equivalent: $G$ has the fewest edges of all connected graphs on $n$ vertices; $G$ is an acyclic connected graph; $G$ is acyclic and has $n - 1$ edges; $G$ is connected and has $n - 1$ edges.
Bipartite graphs
We'll now use the idea of the two colouring of the vertices of a graph to define a bigger class of graphs.
Definition
A graph whose vertices can be coloured in two colours is called a bipartite graph.
Questions
- Find all of the graphs on 3, 4 and 5 vertices that are bipartite.
- In what graphs are the vertices colourable with only one colour? Allow these graphs to be bipartite too.
- Can you give an example of a graph other than P that is three colourable?
- Find the bipartite graphs on 3, 4 and 5 vertices that have the most edges.
Another way of looking at two-colourable graphs is to first divide the vertex set of the graphs into two sets $X$ and $Y$. Then a graph is bipartite if all the edges of the graph join a vertex in $X$ to a vertex in $Y$. The complete bipartite is the graph with all possible edges drawn between $X$ and $Y$. The notation for such graphs is $K_{|X|,|Y|}$.
Questions
- Show that the X, Y definition and the two colourable definition of bipartite graphs are equivalent.
- Draw $K_{2,2}, K_{2,3}, K_{2,5}$.
- What is the complement of $K_{m,n}$?
- How many edges does $K_{m,n}$ have?
- List the sizes of all the cycles in $K_{2,2}, K_{2,3}, K_{2,5}, K_{3,4}, K_{3,6}, K_{1,5}, K_{4,4}$.
- List the sizes of all the cycles in $K_{m,n}$.
- In view of your results from the last Question, make some conjectures about the size of cycles in bipartite graphs. Can you prove these conjectures? How do your conjectures/theorems prove that trees are bipartite?
In Q85 you may have realised that bipartite graphs cannot have odd cycles. We prove that now.
Theorem
A graph is bipartite if and only if it has no odd cycles.
Proof
Suppose that $B$ is bipartite and has an odd cycle. As we have seen in Question 72, an odd cycle requires 3 colours. So if $B$ has an odd cycle it can't be bipartite.
Here's the curly part of the proof. It might help considerably if you draw some pictures to help you see what we're saying here. (In fact by now you should have drawn lots of pictures to help you see what is going on. Drawing pictures is an important tool in graph theory.) Suppose that $G$ is a graph with no odd cycles. Consider any component of $G$. Let $u$ be a vertex of this component. Let $X$ be the set of all vertices $w$ such that the shortest path from $u$ to $w$ is even. Note that $u$ is in $X$. Let $Y$ be the set of all vertices $w$ such that the shortest path from $u$ to $w$ is odd.
Since $V(G) = X \cup Y$, then if we can show that there is no edge between vertices of $X$ or vertices of $Y, X$ and $Y $will be a bipartition of $G$. So we will assume that there is an edge between vertices $u_1$ and $u_2$ of $X$ and produce a contradiction. A similar proof will show that no two vertices of $Y$ are adjacent. Now let $Q$ and $R$ be shortest paths from $u$ to $u_1$ and $u$ to $u_2$, respectively. Suppose that $z$ is the last vertex that $Q$ and $R$ have in common. Then the part of $Q$ from $u$ to $z$ is one of the shortest paths from $u$ to $z$. (Otherwise the paths $Q$ from $u$ to $u_1$ and $R$ from $u$ to $u_2$, would not be shortest paths from $u$ to $u_1$ and $u$ to $u_2$, respectively.) So the subpaths of $Q$ and $R$ from $z$ to $ u_1$ and from $z$ to $u_2$ have the same length. These paths along with the edge $u_1u_2$ form an odd cycle. This is our contradiction.
$\Box$
Corollary
All trees are bipartite.
Proof
Trees are acyclic graphs so they have no odd cycles. They are therefore bipartite.
$\Box$
5'Acyclic' means has no cycles.
6We will assume here that a tree is acyclic and connected
