Content

Isomorphism

The fundamental issue raised by Question 10 and 11 is, when are two graphs the same? This leads us to a fundamental idea in graph theory: isomorphism. If two graphs are the same they are isomorphic. But how do you tell if two graphs are isomorphic? Well the low brow way is to move the vertices of one onto the vertices of another in such a way that the edges of both overlap the edges of the other. If this is possible, then the two graphs are said to be the same, isomorphic. If you can't then they're not. Have a look at Figure 4.

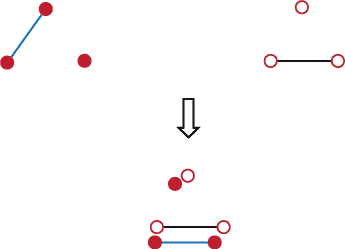
Showing the isomorphism of two graphs

The pictures show how to move the `closed red' vertices onto the `open red' ones so that the single edges of each graph line up. So the two graphs above are isomorphic. As a result the only graphs on three vertices are those with no edges, one edge, two edges and three edges. C in Question 11 is the correct answer.

So two graphs that are the same are said to be isomorphic. But we have to get highbrow and formalise this matter of isomorphism. The rough idea from the answers to Question 11, means that vertices of one graph go to vertices of the other. What's more it shows that the edges of one graph go to the edges of the other and non-edges go to non-edges. We can do this formalisation by a function from the vertices of one graph to the other that sends edges to edges and non-edges to non-edges. We hope the following formal definition is never asked for in an exam because there are far more important things to worry about. But here it is. Two graphs $G$ and $H$ are isomorphic if there is a one-to-one onto function (a bijection) $f$ between the vertices of $G$ and $H$ such that there is an edge between vertices $u$ and $v$ in $G$ if and only if there is an edge between the vertices $f(u) $and $f(v)$ in $H$. So first for every vertex of $G$ there is a corresponding vertex of $H$ and vice versa. And second, every edge of $G$ corresponds to an edge of $H$ and vice versa. That also means that non-edges go to non-edges. We write $G \cong H$ to indicate that $G$ and $H$ are isomorphic.

The isomorphism of graphs can trip you up, especially at the start. A particular graph can be drawn in more than one way so watch out for this. For instance, the apparently two different graphs shown in Figure 5 are actually isomorphic.

An isomorphic pair of graphs

Formally a bijection between vertices is $a \leftrightarrow u, b \leftrightarrow v, c \leftrightarrow x$, and $d \leftrightarrow w$ and between edges is $ab \leftrightarrow uv, ac \leftrightarrow ux, bd \leftrightarrow vw$. Using this bijection we can successfully `sit' the right graph on top of the left graph so that edges sit on the top of edges.

While we are thinking about isomorphism, it turns to be extremely difficult to tell when two graphs with even a reasonable number of edges are isomorphic. This difficulty is called the Isomorphism Problem for Graphs. See https://en.wikipedia.org/wiki/Graph_isomorphism _problem#State_of_the_art. Finding an isomorphism between two graphs is often very important.

Two potentially isomorphic graphs

In the answers we used an idea called `edge-in numbers'. This is something that a student might invent. Now 'edge-in numbers' is ugly, awkward, lengthy and misleading (they are the same as the edge-out numbers after all). So let's introduce a more standard name for these things. These numbers are usually called degrees. So the degrees of the vertices of $G$ are 1, 2, 3 and 2.

From the work on Q15, students should have noticed that the sum of the degrees of a graph is always twice the number of edges. Did they manage to prove that? Did they have a better way than this?

Theorem

The sum of the degrees of a graph is equal to twice the number of edges.

Proof

Look at the edge that goes between vertices $u $and $v$. When we are considering degrees we count this edge once in the degree of $u$ and once in the degree of $v$. So this edge is counted twice in the sum of the degrees. But the same is true for any edge. Hence the result follows.

$\Box$

In the light of the answers to Q11, and to the ideas that have come up in Q26 and Q27, we now want to define the complement of a graph G. The graph $\tilde{G}$ is the complement of $G$ if when $uv$ is an edge of $G$ it isn't an edge of $\tilde{G}$ and vice versa. This is the systematic method that we used in the answer to Q11. Next to a graph in the first column there, in the second column we have listed the complement of that graph. The same thing holds in the third and fourth columns. The graph on its own at the bottom between the third and fourth columns is a special case. It's its own complement. So it's said to be self-complementary.

We have talked already about graphs all of whose vertices have the same degree. In this context another useful word is 'regular'. We say that a graph, with or without loops or multiple edges, is regular if every vertex has the same degree.

The graph in Figure 7 is a regular graph of degree 3. This is the famous Petersen graph. See https://en.wikipedia.org/wiki/Petersen_graph

We'll call this graph $P$. This graph has an important place in graph theory as it turns out to be a counterexample for a lot of conjectures. It is so interesting to graph theorists that a book has been written about it². Even that book doesn't contain everything that is important about the graph.

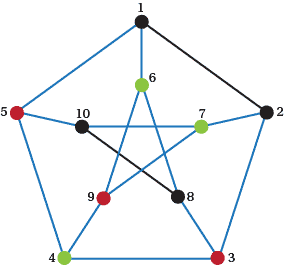
Figure 7: The Petersen graph $P$

We'll get back to $P$ later.

²D. Holton and J Sheehan, 1993, Petersen Graph Theory, Cambridge: Cambridge University Press
³A corollary of a theorem is a result that follows easily from the theorem.
⁴girlfriend

Next page - Content - Trees