Motivation and history

Why would anyone want to look at graph theory and the objects that it look at? How useful is graph theory? We want to look at these first of all from the point of view of the classroom and second from the point of view of the wider world.

In the classroom we can do something with graph theory that is often hard to do with other maths topics — we can show how mathematics develops and how mathematicians approach their subject. This is an important learning experience for students as they are usually given rules to follow and then regurgitate in some form of assessment. They very seldom get a chance to discover mathematical material for themselves. You will see how we attempt to do this as you go through this work.

In the wider world, the answer to the first question leads naturally into the second. As you will soon see as a result of The Walking Problem, graphs can be very easy and straightforward models of objects that simplify more complicated real situations. Once these models have been made they can be tackled more simply than reality and lead to solutions that may be missed or may be harder to find otherwise.

The other day a friend of ours needed to get from their home in Parkville to the corner of Domain and Park Road South Yarra. They picked} up their phone and got onto Google Maps. Immediately they saw a graph with several vertices and edges showing them a few ways that they could make the route. These graphs also included times along various edges. They were then able to take the best route to get them to their destination the best way for them.

Here then are two examples to consider but unfortunately the two graphs used aren't what we call simple graphs, which are the main subject of this site. But if you bear with us, once we get a few ideas out of the way, we'll pick up the application thread for simple graphs in the Applications section. These will include gene technology and assigning people to jobs.

Figure 1: Leonard Euler

But the history of graph theory is interesting too partly because it hasn't yet been around for 300 years. Euler's foray at Königsberg was published in 1736. This is considered to be the birth of the subject as well as being a precursor to topology.

In 1859, Hamilton (see below in the section on circuits) marketed a toy called the Icosahedron Game, where you had to find a path round a (simple) `graph' that went through every `vertex'. This was the beginning of Hamiltonian cycles. Things dribbled on for some time and it wasn't till 1936 that the first textbook on graph theory was published.

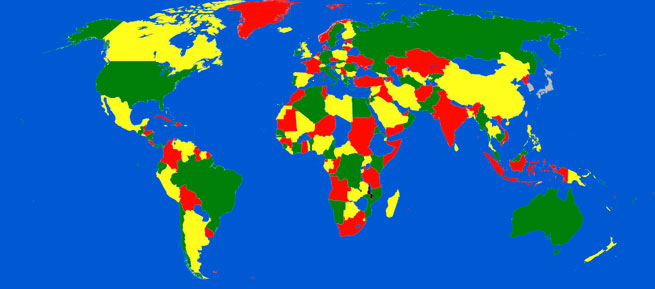
Figure 2: Four colours suffices for any map

Going back a little, in 1852 one Francis Guthrie, a schoolboy, conceived the idea of colouring maps so that no two adjacent countries had the same colour. This was the beginning of over 100 years during which many mathematicians and members of the public tried to show that you needed only 4 colours no matter how many colours your map had or how the relevant graph was arranged. It wasn't until 1976 that Appel and Haken produced a computer aided proof. It was partly because of the spinoff from research on the four colour 'theorem' that graph theory has prospered. But a number of other things were happening that raised the profile of graph theory and generated research in the subject. For more historic pointers, see https://en.wikipedia.org/wiki/Graph_theory.

Next page - Content - A walking problem