Content

Discrete random variables: general ideas

We start with the classic example of rolling a fair six-sided die. This scenario has already been discussed extensively in the module Probability. You may wonder why introductory discussions of probability and random variables often start with examples involving dice, cards and coins. The reason is that these are concrete randomising devices with which we are familiar, and for which we are willing to entertain plausible assumptions about the idealised model.

As we have seen in the module Probability, for coin tossing in particular, this is not as straightforward as it seems. When considering the actual use of dice, cards and coins, the potential for other factors that will invalidate the model should always be kept in mind. Probability and statistics give us the framework to think about this rationally.

But for the initial example, we assume that the model is correct: the die is symmetric in every respect and is shaken well before it is rolled. The uppermost face is observed. The event space for this random procedure is \(\mathcal{E} = \{1,2,3,4,5,6\}\), and the possible outcomes are equiprobable.

Define the discrete random variable \(X\) to be the number on the uppermost face when the die comes to rest. In this case, there is a distinct value of the random variable for each distinct possible outcome of the random procedure. \(X\) can take the values \(1,2,3,4,5,6\), and no other values. It takes discrete values, integers in this case — the die cannot end up with an outcome of \(\pi\) or 1.01 — so \(X\) is a discrete random variable. Since \(X\) can only take six possible values, it is a simple random variable.

The probability that a discrete random variable \(X\) takes the value \(x\) is denoted \(\Pr(X=x)\). We read this as `the probability that \(X\) equals \(x\)', which means the probability that \(X\) takes the value \(x\) when we actually obtain an observation. For the die-rolling example,

\[ \Pr(X = x) = \begin{cases}^\frac{1}{6} &\text{if \(x=1,2,3,4,5,6\),} \\ 0 &\text{otherwise,} \end{cases} \]

for each real number \(x\). Often, for discrete random variables, it is sufficient to specify in some way the values with non-zero probability only; the values with zero probability are usually clear, or clearly implied.

There are other simple random variables that can be defined for the random procedure of rolling a die. For example:

• Let \(Y\) be the number of even numbers appearing. Then \(Y\) takes value 1 if a 2, 4 or 6 is rolled, and \(Y\) takes value 0 otherwise.
• Let \(Z\) be the number of prime numbers appearing. Here \(Z\) takes value 1 if a 2, 3 or 5 is rolled, and takes value 0 otherwise.

These two examples are not terribly interesting; but they illustrate the important point that a single random procedure can accommodate several random variables. Note that "\({Y = 1}\)" and "\({Z = 0}\)" are events, in that they define subsets of the event space \(\mathcal{E}\). The event "\({Y = 1}\)" is \(\{2,4,6\}\). This is a crucial insight; it makes it feasible to obtain the probability distribution of a random variable.

This leads to the definition of a random variable from a formal perspective. Students accustomed to formal mathematical treatments of topics sometimes find the description of a random variable given so far somewhat elusive. A random variable can be defined formally in a way that strongly relates to mathematical topics that students have covered elsewhere, specifically, functions.

A random variable is a numerical-valued function that maps the event space \(\mathcal{E}\) to the set of real numbers. Students will not be familiar with a `variable' that is a function. It is an important conceptual point, represented in the following diagram.

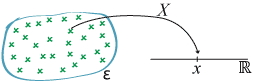
Detailed description
A random variable as a function from the event space \(\mathcal{E}\) to the set \(\mathbb{R}\) of real numbers.

From this diagram, we see that the random variable must take exactly one value for each element of the event space \(\mathcal{E}\). So each possible outcome in the event space has a corresponding value for the random variable. As with functions generally, a number of possible outcomes in \(\mathcal{E}\) may have the same value of the random variable, and in practice this occurs frequently.

Next page - Content - Probability functions