Content

Useful properties of probability

We now look at some of the consequences of the three axioms of probability given in the previous section.

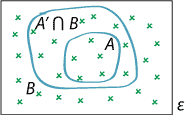
Event \(A\) is a subset of event \(B\).
Detailed description

Property 1

If the event \(A\) is a subset of the event \(B\), then \(\Pr(A) \leq \Pr(B)\). That is,

\[ A \subseteq B \ \implies \ \Pr(A) \leq \Pr(B). \]

Proof

• Consider events \(A\) and \(B\) such that \(A \subseteq B\), as shown in the diagram above. Then \(B = A \cup (A' \cap B)\), and the events \(A\) and \(A' \cap B\) are mutually exclusive. Thus, by the third axiom, \(\Pr(B) = \Pr(A) + \Pr(A' \cap B)\). The first axiom tells us that \(\Pr(A' \cap B) \geq 0\). Hence, \(\Pr(A) \leq \Pr(B)\).

\(\Box\)

This property has a useful application. We write \(A \Rightarrow B\) to mean that, if \(A\) occurs, then \(B\) occurs. So \(A \Rightarrow B\) is the same as \(A \subseteq B\), which implies \(\Pr(A) \leq \Pr(B)\). For example:

• Indiana Jones can only find the treasure (\(A\))
• if he first solves the puzzle of the seven serpents (\(B\));

so \(A \subseteq B\) and therefore \(\Pr(A) \leq \Pr(B)\); his chance of finding the treasure is at most equal to his chance of solving the puzzle.

While property 1 is important, it is rather obvious.

Property 2

\(0 \leq \Pr(A) \leq 1\), for each event \(A\).

Proof

• The first axiom says that \(\Pr(A) \geq 0\). It is true for every event \(A\) that \(A \subseteq \mathcal{E}\). Hence \(\Pr(A) \leq \Pr(\mathcal{E})\), by property 1. But \(\Pr(\mathcal{E}) = 1\), by the second axiom, and so it follows that \(\Pr(A) \leq 1\).

\(\Box\)

This property formalises the scale for probabilities, given the axioms.

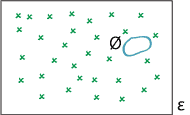
The empty event.
Detailed description

Property 3

\(\Pr(\varnothing) = 0\).

Proof

• Choose any event \(A\). Then the two events \(A\) and the empty set \(\varnothing\) are mutually exclusive, so \(\Pr(A \cup \varnothing) = \Pr(A) + \Pr(\varnothing)\), by the third axiom. Since \(A \cup \varnothing = A\), this gives \(\Pr(A) = \Pr(A) + \Pr(\varnothing)\). Hence, \(\Pr(\varnothing) = 0\).

\(\Box\)

It would be rather strange if the probability of the empty set was anything other than zero, so it is reassuring to confirm that this is not so: \(\Pr(\varnothing) = 0\), as expected.

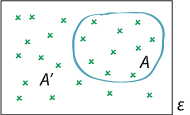
An event \(A\) and its complementary event \(A'\).
Detailed description

Property 4

\(\Pr(A') = 1 - \Pr(A)\), for each event \(A\).

Proof

• The events \(A\) and \(A'\) are mutually exclusive, so \(\Pr(A \cup A') = \Pr(A) + \Pr(A')\), by the third axiom. But \(A \cup A' = \mathcal{E}\), and therefore \(\Pr(A') = \Pr(\mathcal{E}) - \Pr(A)\). According to the second axiom, \(\Pr(\mathcal{E}) = 1\). Hence, \(\Pr(A') = 1 - \Pr(A)\).

\(\Box\)

This property is surprisingly useful and is applied frequently. It is most effective when the probability of the event of interest is difficult to calculate directly, but the probability of the complementary event is known or easily calculated.

Property 5 (Addition theorem)

\(\Pr(A \cup B) = \Pr(A) + \Pr(B) - \Pr(A \cap B)\), for all events \(A\) and \(B\).

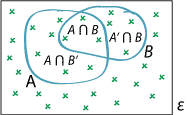Detailed description		\(B\) \(B'\) \(A\) \(A \cap B\) \(A \cap B'\) \(A'\) \(A' \cap B\) \(A' \cap B'\)
Two representations of the addition theorem.

Both the diagram and the table above give representations of the event space \(\mathcal{E}\) in terms of the two events \(A\) and \(B\) and their complements.

The impression we get from the diagram, from the table, or just using basic logic is that, if we add together the probability of \(A\) and the probability of \(B\), then \(A \cap B\) is included in both events, so it has been counted twice. Hence, to obtain the probability of at least one of \(A\) and \(B\) occurring, that is, to obtain \(\Pr(A \cup B)\), we need to subtract \(\Pr(A \cap B)\) from \(\Pr(A) + \Pr(B)\). This justifies the formula given by the addition theorem (property 5). We can demonstrate the result more formally, as follows.

Proof

• To devise a formal proof of the addition theorem, we construct mutually exclusive events in a helpful way, and use the third axiom of probability.
  
  We can express the union of \(A\) and \(B\) as \(A \cup B = A \cup (A' \cap B)\), and the events \(A\) and \(A' \cap B\) are mutually exclusive. Also, \(B = (A \cap B) \cup (A' \cap B)\), and the two events \(A \cap B\) and \(A' \cap B\) are mutually exclusive. By applying the third axiom to the first of these relationships, we get that \[ \Pr(A \cup B) = \Pr(A) + \Pr(A' \cap B). \] And using the third axiom for the second relationship, we find that \begin{align*} \Pr(B) &= \Pr(A \cap B) + \Pr(A' \cap B)\\ \implies \ \Pr(A' \cap B) &= \Pr(B) - \Pr(A \cap B). \end{align*} Hence, \(\Pr(A \cup B) = \Pr(A) + \Pr(B) - \Pr(A \cap B)\), as required.

\(\Box\)

Next page - Content - Assigning probabilities