Links forward

Bisection and binary numbers

The binary number system is in many ways well suited to the bisection method.

To see why, suppose we are searching for a solution to $f(x) = 0$ in the interval $[0, 32]$, and suppose there is a unique solution $x=19$ (although we don't know that yet!).

Using the bisection method, we will obtain several intervals $[a_n, b_n]$, and when we arrive at $x=19$, we will discover that we have found the solution exactly. We can write out these intervals; we do so in both decimal and binary notation.

Interval	$[a_0, b_0]$	$[a_1, b_1]$	$[a_2, b_2]$	$[a_3, b_3]$	$[a_4, b_4]$
Decimal	$[0, 32]$	$[16, 32]$	$[16, 24]$	$[16, 20]$	$[18, 20]$
Binary	[0, 100000]	[10000, 100000]	[10000, 11000]	[10000, 10100]	[10010, 10100]

We illustrate these intervals below, denoting binary numbers with a subscript $2$. As in previous illustrations, the intervals $[a_n,b_n]$ are shown in green and the solution in red.

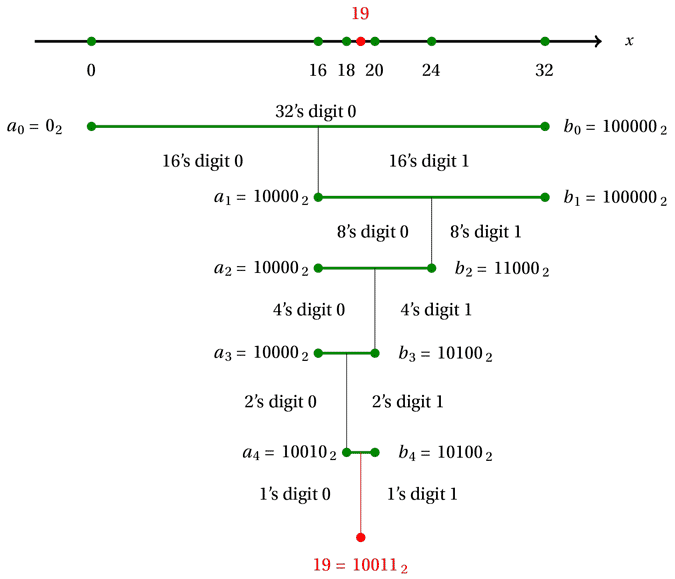
At the first step, we split the interval from $0$ to $32$ at the midpoint $16$. Now the numbers from $0$ to $16$ are precisely those which have a $0$ in the 16's digit, and the numbers from $16$ to $32$ are those which have a $1$ in the 16's digit. Therefore, at the first step of the bisection algorithm, we determine the $16$'s digit of the solution. Since in our example $[a_1, b_1] = [16, 32]$ on the right, the solution has a $1$ in the 16's digit.

At the second step, we split the interval from $16$ to $32$ at the midpoint $24$; the lower half (from $16$ to $24$) consists of numbers with a $0$ in the $8$'s digit, and the upper half (from $16$ to $32$) consists of numbers with a $1$ in the $8$'s digit. So at the second step of the bisection method, we determine the $8$'s digit of the solution. Since $[a_2, b_2]$ is the lower half $[16, 24]$, the solution has a $0$ in the 8's digit.

Continuing in this way, each step of the bisection method provides another binary digit of the solution. The next interval $[a_3, b_3]$ is the lower half of $[a_2, b_2]$, so the solution has a $0$ in the $4$'s digit. Then $[a_4, b_4]$ is the upper half of $[a_3, b_3]$, so the solution has a $1$ in the $2$'s digit. Finally we arrive at the solution, which is $10011$ in binary.

Provided that we start from an interval which fits nicely with the binary number system, each step of the bisection algorithm determines a further binary digit of the solution. This continues even when we consider fractions: we determine binary digits which appear after the "decimal" point.

The bisection method is well suited to the binary, or base 2 number system, because it splits the interval at each stage into two pieces, which can align with binary digits.

The bisection method is less well suited to the decimal number system. The intervals $[a_n, b_n]$ do not correspond nicely to decimal digits. As we have found previously, the number of iterations required to find a solution to a desired number of decimal places can vary rather haphazardly.

Next page - Links forward - Complex numbers and Newton fractals