History and applications

Sir Isaac Newton (1642–1727)

Newton was a central figure in the scientific revolution, and arguably the greatest mathematician and greatest physicist of all time. On one occasion, he claimed with false modesty: 'If I have seen further it is by standing on the shoulders of giants.' Certainly, he studied the work of Galileo, Copernicus, Kepler, Fermat and Descartes, among others.

He began his serious study of calculus in the mid 1660s, partly at his family home in Wolsthorpe when he was forced to leave Cambridge because of the great plague of 1665. He instigated a study of fluxions of a given fluent. The fluxion is the derivative of a function, which Newton called the fluent. He began his study by finding power-series representations of many functions. For example,

\[ \sqrt{1+t^2} = 1 + \dfrac{t^2}{4} - \dfrac{t^4}{8} + \dfrac{t^6}{16} - \dfrac{5t^8}{128} + \dotsb, \qquad\text{for } -1 < t < 1. \]

To obtain the fluxion, all he had to do was to differentiate the power series term-by-term. Newton, however, was much more interested in curves than in functions.

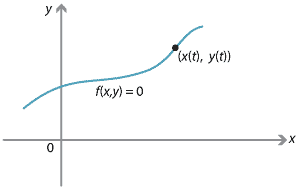
He always thought of \(t\) as time, although in modern language, \(t\) is a parameter. Thus we may think of motion in a straight line, \(x(t)\), as the principal subject of Newton's calculus. It is this context that motivated Newton to study both differential and integral calculus. Newton listed two central problems in his Treatise on methods:

'Given the length of the space continuously (that is, at every time), to find the speed of the motion at any time proposed.'
'Given the speed of motion continuously, to find the length of the space described at any time proposed.'

In modern terms, these problems are:

Given \(x(t)\), find \(v(t) = \dfrac{dx(t)}{dt}\).
Given \(v(t)\), find \(x(t) = \displaystyle\int v(t)\,dt\).

As noted earlier, Newton's independent variable is always \(t\). As an example of his ideas, Newton took a curve \(f(x,y) = 0\) with \(x = x(t)\) and \(y = y(t)\), and invented a procedure equivalent to what is today written as

\[ \dfrac{\partial f}{\partial x} \dfrac{dx}{dt} + \dfrac{\partial f}{\partial y}\dfrac{dy}{dt} = 0. \]

He also wrote down a simplified table of integrals which did not include logarithmic, exponential or trigonometric functions.

By the 1670s, Newton had started work on kinematics, and clarified the ideas of position (displacement), velocity and acceleration, using calculus to relate them. He also introduced the concepts of force, momentum, energy and power. In 1687, he published the most important mathematical book to appear up to that time. It is known as Principia, but its full title is Philosophiae naturalis principia mathematica (Mathematical principles of natural philosophy). This book includes Newton's famous three laws of motion, which he took as axioms:

Every body perseveres in its state of being at rest or of moving uniformly straight forward, except insofar as it is compelled to change its state by forces impressed. (This is the law of conservation of momentum.)
A change in motion is proportional to the motive force impressed and takes place along the straight line in which that force is impressed. (This is the law \(F = ma\) or, expressed as a vector equation, \(\mathbf{F} = m\mathbf{a}\).)
To any action there is always an equal and opposite reaction.

From these three laws, Newton derived Kepler's second law: the area swept out is proportional to time. He then effectively stated his universal law of gravitation,

\[ F = \dfrac{G m_1 m_2}{d^2}, \]

and derived Kepler's first and third laws. Kepler's laws were actually conjectures based on astronomical observations. Newton's genius was to derive them from his axioms.

Next page - History and applications - Kinematics after Newton