Content
Constant acceleration
We are all familiar with the fact that a car speeds up when we put our foot down on the accelerator. The rate of change of the velocity of a particle with respect to time is called its acceleration. If the velocity of the particle changes at a constant rate, then this rate is called the constant acceleration.
Since we are using metres and seconds as our basic units, we will measure acceleration in metres per second per second. This will be abbreviated as m/s\(^2\). It is also commonly abbreviated as ms\(^{-2}\).
For example, if the velocity of a particle moving in a straight line changes uniformly (at a constant rate of change) from 2 m/s to 5 m/s over one second, then its constant acceleration is 3 m/s\(^2\).
Example
Let \(t\) be the time in seconds from the beginning of the motion of a particle. If the particle has a velocity of 4 m/s initially (at \(t=0\)) and has a constant acceleration of 2 m/s\(^2\), find the velocity of the particle:
- when \(t=1\)
- when \(t=2\)
- after \(t\) seconds.
Draw the velocity–time graph for the motion.
Solution
- When \(t=1\), the velocity of the particle is \(4 + 2 = 6\) m/s.
- When \(t=2\), the velocity of the particle is \(4 + 2 \times 2 = 8\) m/s.
- After \(t\) seconds, the velocity of the particle is \(4 + 2t\) m/s.
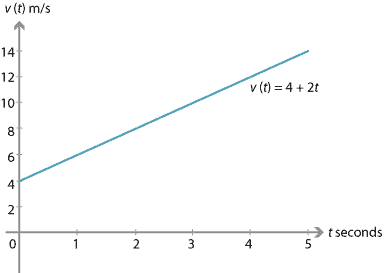
Decreasing velocity
If the velocity of a particle moving in a straight line changes uniformly (at a constant rate of change) from 5 m/s to 2 m/s over one second, its constant acceleration is \(-3\) m/s\(^2\).
If a particle has an initial velocity of 6 m/s and a constant acceleration of \(-2\) m/s\(^2\), then:
- when \(t=1\), the velocity of the particle is 4 m/s
- when \(t=2\), the velocity of the particle is 2 m/s
- when \(t=3\), the velocity of the particle is 0 m/s
- when \(t=4\), the velocity of the particle is \(-2\) m/s
- when \(t=10\), the velocity of the particle is \(-14\) m/s.
In general, the velocity of the particle is \(6-2t\) m/s after \(t\) seconds. The velocity–time graph for this motion is shown below; it is the graph of \(v(t)=6-2t\).
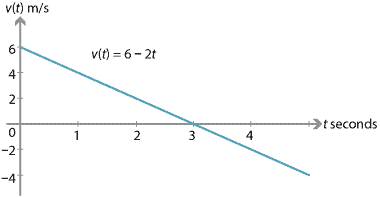
Over the first three seconds, the particle's speed is decreasing (the particle is slowing down). At three seconds, the particle is momentarily at rest. After three seconds, the velocity is still decreasing, but the speed is increasing (the particle is going faster and faster).
Summary
If we assume that the rate of change of velocity (acceleration) is a constant, then the constant acceleration is given by
\[ \text{Acceleration} = \dfrac{\text{Change in velocity}}{\text{Change in time}}. \]More precisely, the constant acceleration \(a\) is given by the formula
\[ a = \dfrac{v(t_2)-v(t_1)}{t_2-t_1}, \]where \(v(t_i)\) is the velocity at time \(t_i\). Since velocity is a vector, so is acceleration.
Example
A particle is moving in a straight line with constant acceleration of 1.5 m/s\(^2\). Initially its velocity is 4.5 m/s. Find the velocity of the particle:
- after 1 second
- after 3 seconds
- after \(t\) seconds.
Solution
- After 1 second, the velocity is \(4.5 + 1.5 = 6\) m/s.
- After 3 seconds, the velocity is \(4.5 + 3\times 1.5 = 9\) m/s.
- After \(t\) seconds, the velocity is \(4.5 + 1.5t\) m/s.
Example
A car is travelling at 100 km/h \(= \dfrac{250}{9}\) m/s, and applies its brakes to stop. The acceleration is \(-10\) m/s\(^2\). How long does it take for the car to stop?
Solution
After one second, the car's velocity is \(\dfrac{250}{9} - 10\) m/s. After \(t\) seconds, its velocity is
\[ v(t) = \dfrac{250}{9} - 10t \text{ m/s}. \]The car stops when \(v(t) = 0\). Solving this equation gives
\begin{align*} \dfrac{250}{9} - 10t &= 0 \\ t &= \dfrac{25}{9}. \end{align*}The car takes approximately 2.8 seconds to stop.
(In exercise 6, we will find out how far the car travels during this time.)
The constant-acceleration formulas for motion in a straight line
Throughout this section, we have been considering motion in a straight line with constant acceleration. This situation is very common; for example, a body moving under the influence of gravity travels with a constant acceleration.
There are five frequently used formulas for motion in a straight line with constant acceleration. The formulas are given in terms of the initial velocity \(u\), the final velocity \(v\), the displacement (position) \(x\), the acceleration \(a\) and the time elapsed \(t\). Of course, they require consistent systems of units to be used.
It is assumed that the motion begins when \(t = 0\), and that the initial position is taken as the origin, that is, \(x(0) = 0\).
The five equations of motion
- \(v = u + at\)
- \(x = \dfrac{(u+v)t}{2}\)
- \(x = ut + \dfrac{1}{2}at^2\)
- \(v^2 = u^2 + 2ax\)
- \(x = vt - \dfrac{1}{2}at^2\)
Note. Each of the five equations involve four of the five variables \(u, v, x, a, t\). If the values of three of the variables are known, then the remaining values can be found by using two of the equations.
Deriving the constant-acceleration formulas
The first equation of motion
Since the acceleration is constant, we have \(a = \dfrac{v-u}{t}\). This gives the first equation of motion, \(v = u + at\).
The second equation of motion
The second equation,
\[ x = \dfrac{(u+v)t}{2}, \]says that displacement is obtained by multiplying the average of the initial and final velocities by the time elapsed during the motion. More simply:
\[ \text{Displacement} = \text{Average velocity} \times \text{Time taken}. \]We can derive this equation using the fact that the displacement is equal to the signed area under the velocity–time graph.
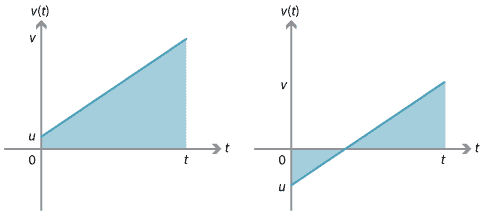
For the velocity–time graph on the left, the region under the graph is a trapezium. The displacement \(x\) is equal to the area of the trapezium, which is \(\dfrac{1}{2}(u+v)t\). So the second equation of motion holds in this case.
For the graph on the right, the displacement can be found by considering the two triangles between the graph and the \(t\)-axis. One of the triangles has positive signed area and the other has negative signed area.
Finding the displacement of a particle from the velocity–time graph using integration will be discussed in a later section of this module.
The third equation of motion
Substituting for \(v\) from the first equation into the second equation gives
\begin{align*} x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(u+u+at)t}{2} \\ &= \dfrac{2ut+at^2}{2} \\ &= ut + \dfrac{1}{2}at^2, \end{align*}which is the third equation. Thus \(x\) is a quadratic in \(t\), and hence the graph of \(x\) against \(t\) is a parabola.
The fourth equation of motion
From the first equation, we have \(t = \dfrac{v-u}{a}\). Substituting this into the second equation gives
\begin{align*} x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(u+v)(v-u)}{2a} \\ &= \dfrac{v^2-u^2}{2a}. \end{align*}Rearranging to make \(v^2\) the subject produces the fourth equation: \(v^2 = u^2 + 2ax\).
The fifth equation of motion
From the first equation, we have \(u = v-at\). Using the second equation, we obtain
\begin{align*} x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(v-at+v)t}{2} \\ &= \dfrac{2vt-at^2}{2} \\ &= vt-\dfrac{1}{2}at^2, \end{align*}which is the fifth equation.
Exercise 2
Derive the third and fifth equations of motion from a velocity–time graph. (For simplicity, you may assume that both \(u\) and \(v\) are positive.)
Vertical motion
Motion due to gravity is a good context in which to demonstrate the use of the constant-acceleration formulas. As discussed earlier, our two directions in vertical motion are up and down, and a decision has to be made as to which of the two directions is positive. Acceleration due to gravity is a constant, with magnitude denoted by \(g\). In the following example, we take the upwards direction to be positive and take \(g = 10\) m/s\(^2\).
Example
A stone is launched vertically upwards from ground level with the initial velocity 30 m/s. Assume that the acceleration is \(-10\) m/s\(^2\).
- Find the time taken for the stone to return to the ground again.
- Find the maximum height reached by the stone.
- Find the velocity with which it hits the ground.
- Sketch the position–time graph and the velocity–time graph for the motion.
- Find the distance covered by the stone from the launch to when it returns to earth.
Solution
In this example, we have \(u=30\) and \(a=-10\), with up as the positive direction.
- Using the third equation of motion, \(x = ut+\dfrac{1}{2}at^2\), we have \(x = 30t-5t^2\). To find the time taken to return to the ground, we substitute \(x=0\) to obtain \begin{align*} 0 &= 30t-5t^2 \\ 0 &= 5t(6-t). \end{align*} Therefore \(t=0\) or \(t=6\). Thus the time taken to return to the ground is 6 seconds.
- We can find the maximum height using the fourth equation of motion, \(v^2 = u^2+2ax\). When the stone reaches the highest point, \(v=0\). So we have \begin{align*} 0 &= 900 - 20x \\ x &= 45. \end{align*} Hence, the maximum height reached by the stone is 45 metres.
- The stone hits the ground when \(t=6\). Using the first equation of motion, \[ v = 30 - 10\times 6 = -30 \text{ m/s}. \]
- From the third equation of motion, we have \(x(t) = 30t-5t^2\).
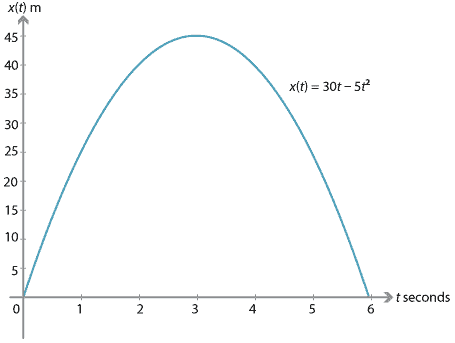
The first equation of motion gives \(v(t) = 30-10t\).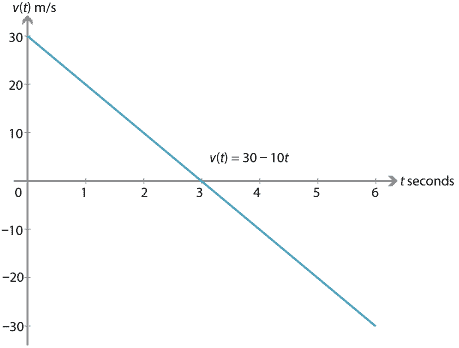
- The maximum height reached by the stone is 45 m, and so the stone travels a distance of 90 m.
Notes.
- Another way to find the maximum height is by using the position–time graph. The graph of \(x(t)\) is a parabola with \(t\)-intercepts 0 and 6. Hence, the maximum value of \(x(t)\) occurs when \(t=3\). It follows that the maximum height reached by the stone is \(x(3) = 30\times 3 - 5\times 3^2 = 45\) metres.
- Looking at the velocity–time graph, we can see that the triangle above the \(t\)-axis has a signed area of 45 and the triangle below the \(t\)-axis has a signed area of \(-45\). Thus, when the stone has returned to ground level, it has travelled 90 m but its displacement is zero.
In the previous example, we took \(-10\) m/s\(^2\) as the approximate acceleration due to gravity. A more accurate value is \(-9.8\) m/s\(^2\). Use this value in the following exercise.
Exercise 3
A man dives from a springboard where his centre of gravity is initially 12 metres above the water, and his initial velocity is 4.9 m/s upwards. Regard the diver as a particle at his centre of gravity, and assume that the diver's motion is vertical.
- Find the diver's velocity after \(t\) seconds (up to when he hits the water).
- Find the diver's height above the water after \(t\) seconds (up to when he hits the water).
- Find the maximum height of the diver above the water.
- Find the time taken for the diver to reach the water.
- Sketch the velocity–time graph for this motion (up to when he hits the water).
- Sketch the position–time graph for this motion (up to when he hits the water).
Exercise 4
A body projected upwards from the top of a tower reaches the ground in \(t_1\) seconds. If projected downwards with the same speed, it reaches the ground in \(t_2\) seconds. Prove that, if simply let drop, it would reach the ground in \(\sqrt{t_1t_2}\) seconds.
Exercise 5
A particle is dropped from a tower of height \(h\). At the same time, a particle is projected upwards with a velocity from the bottom the tower. They meet when the particle dropped from the top has travelled a distance of \(\smash{\dfrac{h}{n}}\). Show that the velocities when they meet are in the ratio \(2 : 2-n\), and that the initial velocity of the second particle is \(\sqrt{\dfrac{ngh}{2}}\).
Further use of the equations of motion
Example
A car accelerates uniformly (constant acceleration) from 0 m/s to 30 m/s in 12 seconds, and continues to accelerate at the same rate. Find
- the acceleration
- the time it will take for the car to increase its velocity from 30 m/s to 80 m/s
- the distance the car travels in the first 30 seconds of motion.
Solution
- Use the first equation of motion, \(v = u + at\). Substituting \(u=0\), \(v=30\) and \(t = 12\) gives \(30 = 12a\). Hence, the acceleration is \(a = \dfrac{5}{2}\) m/s\(^2\).
- Use the first equation of motion again, with \(u=30\) and \(v=80\): \[ 80 = 30 + \dfrac{5}{2}t. \] Thus \(t = 20\) seconds.
- Use the third equation of motion, \(x = ut + \dfrac{1}{2}at^2\). Substitute \(u=0\), \(a=\dfrac{5}{2}\) and \(t=30\): \[ x = \dfrac{1}{2} \times \dfrac{5}{2} \times 30^2 = 1125 \text{ metres}. \] The car travels 1125 metres in the first 30 seconds of motion.
Exercise 6
A car is travelling at 100 km/h \(= \dfrac{250}{9}\) m/s. It brakes and slows down with an acceleration of \(-10\) m/s\(^2\). How far, to the nearest metre, does it go before it stops?
Exercise 7
A car accelerates from 0 km/h to 100 km/h in 10 seconds, and continues for 40 seconds at 100 km/h. The driver then brakes strongly to stop in 38 metres.
- Convert 100 km/h to m/s.
- Find the constant acceleration of the car for the first 10 seconds in m/s\(^2\).
- Find the total distance travelled by the car in metres.
- Find the acceleration for the braking phase in m/s\(^2\).
- How long does it take the car to stop from when the brakes are first applied?
- Sketch a velocity–time graph for the motion of the car.
