Content

Position, displacement and distance

In this module, we are only talking about motion in a straight line. For a horizontal line, there are only two directions to consider: right and left. For a vertical line, the two directions are up and down. We choose a point \(O\) on the line, which we call the reference point or origin. For convenience, we will measure distance in metres and time in seconds.

Position

The line is coordinatised and referenced from a point \(O\), the origin. For a horizontal line, the convention is that positions to the right of \(O\) are positive, and positions to the left are negative.

For example:

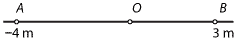
The position of the particle at \(B\) is 3 m.
The position of the particle at \(A\) is \(-4\) m.

The position of a particle is often thought of as a function of time, and we write \(x(t)\) for the position of the particle at time \(t\).

Displacement

The displacement of a particle moving in a straight line is the change in its position. If the particle moves from the position \(x(t_1)\) to the position \(x(t_2)\), then its displacement is \(x(t_2) - x(t_1)\) over the time interval \([t_1,t_2]\). In particular, the position of a particle is its displacement from the origin.

For example:

If a particle moves from \(O\) to \(B\), its displacement is 3 m.
If a particle moves from \(O\) to \(A\), its displacement is \(-4\) m.
If a particle moves from \(A\) to \(B\), its displacement is 7 m.
If a particle moves from \(B\) to \(A\), its displacement is \(-7\) m.

Position and displacement are vector quantities, that is, they have both magnitude and direction. In this module, we are dealing with vectors in one dimension. The sign of the quantity (positive or negative) indicates its direction. The absolute value of the quantity is its magnitude.

Distance

The distance is the 'actual distance' travelled. Distances are always positive or zero.

For example, given the following diagram, if a particle moves from \(A\) to \(B\) and then to \(O\), the displacement of the particle is 4 m, but the distance travelled is 10 m.

Example

A particle moves along a straight line so that its position at time \(t\) seconds is \(x(t)\) metres, relative to the origin. Assume that \(x(0) = 0\), \(x(3) = 2\) and \(x(6) = -5\), and that the particle only changes direction when \(t = 3\). Find the distance travelled by the particle from time \(t = 0\) to time \(t = 6\).

Solution

The distance travelled is \(2 + 7 = 9\) metres.

Summary

The position of a particle moving in a straight line is a vector which represents a point \(P\) on the line in relation to the origin \(O\). The position of a particle is often thought of as a function of time, and we write \(x(t)\) for the position of the particle at time \(t\).
The displacement of a particle moving in a straight line is a vector defined as the change in its position. If the particle moves from the position \(x(t_1)\) to the position \(x(t_2)\), its displacement is \(x(t_2) - x(t_1)\) for the time interval \([t_1,t_2]\).
The distance travelled by a particle is the 'actual distance' travelled.

Next page - Content - Constant velocity