Answers to exercises

Exercise 1

If \(1 \leq a < b\) and \(h>0\), then \(a^h < b^h\). Subtracting 1 from both sides and dividing by \(h\) (which is positive) gives the first inequality. This inequality holds for all \(h>0\), hence taking a limit as \(h \to 0\), we have the desired inequality. (Note that, in the limit, the strict inequality becomes non-strict.)

Exercise 2
  1. Using the product rule, \(f'(x) = 2x e^x + x^2 e^x = (2x+x^2)e^x\).
  2. Using the chain rule, \(f'(x) = e^{e^x} \cdot e^x = e^{x + e^x}\).
Exercise 3

Differentiating both sides gives

\begin{align*} 1 &= e^{\log_e x} \cdot \dfrac{d}{dx}\, \log_e x \\ &= x \cdot \dfrac{d}{dx}\, \log_e x. \end{align*}

It follows that \(\dfrac{d}{dx} \, \log_e x = \dfrac{1}{x}\).

Exercise 4

Using the chain rule,

\[ f'(x) = \dfrac{1}{-x} \cdot (-1) = \dfrac{1}{x}. \]

As \(f\) has domain \((-\infty, 0)\) and \(f'\) is defined on this entire interval, the function \(f'\) also has domain \((-\infty, 0)\).

Exercise 5

The function \(f(x)\) is defined when \(3-7x>0\), i.e., \(x < \dfrac{3}{7}\). So the domain is \((-\infty, \dfrac{3}{7})\).

Exercise 6
  1. Writing \(f(x) = e^{\log_e 2 \cdot x^2}\) and using the chain rule gives \begin{align*} f'(x) &= \log_e 2 \cdot 2x \cdot e^{\log_e 2 \cdot x^2}\\ &= \log_e 2 \cdot x \cdot 2^{x^2+1}. \end{align*}
  2. Writing \(f(x) = e^{\log_e 3 \cdot (4x^2 + 2x - 7)}\) and using the chain rule gives \begin{align*} f'(x) &= \log_e 3 \cdot (8x + 2) \cdot e^{\log_e 3 \cdot (4x^2 + 2x - 7)}\\ &= \log_e 3 \cdot (8x+2) \cdot 3^{4x^2 + 2x - 7}. \end{align*}
Exercise 7

From first principles, if \(f(x) = 2^x\), then

\[ f'(0) = \lim_{h \to 0} \dfrac{2^h - 1}{h}. \]

We have now shown that \(f'(x) = \log_e 2 \cdot 2^x\), so \(f'(0) = \log_e 2\). The desired equality follows.

Exercise 8

From first principles, if \(f(x) = a^x\), then

\[ f'(0) = \lim_{h \to 0} \dfrac{a^h - 1}{h}. \]

Knowing now that \(f'(x) = \log_e a \cdot a^x\), and so \(f'(0) = \log_e a\), gives the desired equality.

Exercise 9

Writing

\[ f(x) = x^x = \bigl( e^{\log_e x} \bigr)^x = e^{x \, \log_e x} \] and using the chain and product rules, we obtain \begin{align*} f'(x) &= e^{x \, \log_e x} \cdot \dfrac{d}{dx} (x \, \log_e x)\\ &= x^x \Bigl( x \cdot \dfrac{1}{x} + 1 \cdot \log_e x \Bigr)\\ &= x^x ( 1 + \log_e x ). \end{align*}

The function \(f(x)\) is only defined for \(x>0\), so \(x^x \neq 0\). Thus the stationary points occur precisely when \(\log_e x = -1\), that is, \(x = e^{-1} = \dfrac{1}{e}\).

Exercise 10
  1. First, using the change of base rule, we have \[ f(x) = \dfrac{\log_e (xy)}{\log_e a} \qquad \text{and} \qquad g(x) = \dfrac{\log_e x}{\log_e a} + \dfrac{\log_e y}{\log_e a}. \] So, using the chain rule (and thinking of \(y\) as a constant), we compute \[ f'(x) = \dfrac{1}{\log_e a} \cdot \dfrac{1}{xy} \cdot y = \dfrac{1}{x \, \log_e a} \] and \[ g'(x) = \dfrac{1}{\log_e a} \cdot \dfrac{1}{x} = \dfrac{1}{x \, \log_e a}. \] Hence \(f'(x) = g'(x)\).
  2. Since \(\log_a 1 = 0\), we compute \(f(1) = \log_a y\) and \(g(1) = \log_a y\).
  3. As the functions \(f\) and \(g\) have identical derivatives, they are equal up to a constant. Since \(f(1) = g(1)\), it follows that \(f(x)\) and \(g(x)\) must be equal for all \(x\).
Exercise 11
\begin{align*} \int_1^x \dfrac{1}{t} \; dt &= \bigl[ \log_e t \bigr]_1^x\\ &= \log_e x - \log_e 1 = \log_e x \end{align*}
Exercise 12
\begin{align*} \int_{x^n}^{x^{n+1}} \dfrac{1}{t} \; dt &= \bigl[ \log_e t \bigr]_{x^n}^{x^{n+1}}\\ &= \log_e \bigl( x^{n+1} \bigr) - \log_e \bigl( x^n \bigr) = \log_e \Bigl( \dfrac{x^{n+1}}{x^n} \Bigr) = \log_e x \end{align*}
Exercise 13

Using the product rule, we compute

\[ f'(x) = 1 \cdot \log_e x + x \cdot \dfrac{1}{x} - 1 = \log_e x. \]

Thus \(f(x)\) is an antiderivative of \(\log_e x\), and we have

\[ \int \log_e x \; dx = x \, \log_e x - x + c, \] where \(c\) is a constant of integration.
Exercise 14

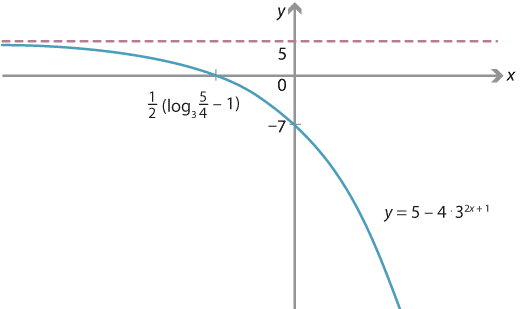
Substituting \(x=0\) gives a \(y\)-intercept of \(5 - 4 \cdot 3 = -7\). Substituting \(y=0\), we obtain \({0 = 5 - 4 \cdot 3^{2x+1}}\), and so \(3^{2x+1} = \dfrac{5}{4}\). Hence the \(x\)-intercept is \(\dfrac{1}{2}( \log_3 \dfrac{5}{4} - 1 ) \approx - 0.4\).

The equation \(y=5 - 4\cdot 3^{2x+1}\) can be written as \(y= -4 g\bigl(2(x+\dfrac{1}{2})\bigr) + 5\), where \(g(x) = 3^x\). Hence the graph here is obtained from the graph of \(y= 3^x\) by applying the following transformations:

Under these transformations, the asymptote moves to \(y=5\).

Graph of y = 5 minus 4 times 3 to the power of 2x + 1.
Detailed description

Exercise 15
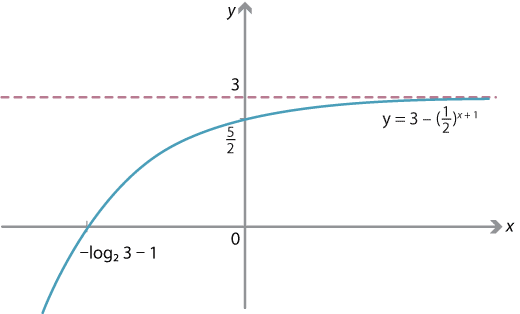
  1. Reflecting the graph of \(y=2^x\) in the \(y\)-axis gives the graph of \(y=2^{-x}\). By the index laws, we see that \(2^{-x} = \bigl( \dfrac{1}{2} \bigr)^x\).
  2. The equation \(y = 3 - \bigl( \dfrac{1}{2} \bigr)^{x+1}\) can be written as \(y=3 - g\bigl(-(x+1)\bigr)\), where \(g(x) = 2^x\). Hence the graph is obtained from that of \(y=2^x\) by the following transformations:
  1. Under these transformations, the asymptote moves to \(y=3\).

Graph of y = 3 minus one half to the power x plus 1.
Detailed description

Exercise 16

Dilating the graph \(y=3^x\) in the \(y\)-direction from the \(x\)-axis with factor 9 gives the graph \(y=9 \cdot 3^x\). Translating the graph \(y=3^x\) by 2 units to the left gives the graph \(y=3^{x+2}\). As \(3^{x+2} = 3^2 \cdot 3^x = 9 \cdot 3^x\), these two graphs are identical.

Exercise 17

To solve the equation \(\log_a x = N\) is as simple as rewriting it as \(x = a^N\). So, yes, \(\log_a x\) does take the value \(N\), for the (very large) value of \(x = a^N\).

Exercise 18

Subtracting the first equation from the second gives \(\log_e(x+10^6) - \log_e x = 1\). Using a logarithm law, this simplifies to

\[ \log_e \Bigl( \dfrac{x+10^6}{x} \Bigr) = 1 \ \implies \ 1 + \dfrac{10^6}{x} = e. \]

Therefore \(x = \dfrac{10^6}{e-1}\) and \(y = \log_e x = \log_e \Bigl( \dfrac{10^6}{e-1} \bigr)\).

Exercise 19

Dilating the graph \(y = \log_3 x\) in the \(x\)-direction from the \(y\)-axis with factor 9 gives the graph \(y = \log_3 \bigl( \dfrac{x}{9} \bigr)\). Translating the graph \(y= \log_3 x\) down by 2 units gives the graph \({y = \log_3 x - 2}\). By the logarithm laws, we have

\[ \log_3 \Bigl( \dfrac{x}{9} \Bigr) = \log_3 x - \log_3 9 = \log_3 x - 2, \] so these two graphs are identical.

The equation \(y= \log_3 x\) is equivalent to \(x = 3^y\); the function \(f(x) = \log_3 x\) is the inverse of the function \(f^{-1}(x) = 3^x\) considered in exercise 16. One graph is obtained from the other by reflection in the line \(y=x\). The two transformations considered here are the mirror images (under reflection in \(y=x\)) of the two transformations considered in exercise 16.

Exercise 20

By our definition, \(f(x) = x^\alpha = \exp(\alpha \, \ln x)\), and so from the chain rule we obtain

\[ f'(x) = \dfrac{\alpha}{x} \, \exp(\alpha \, \ln x) = \dfrac{\alpha}{x} \cdot x^\alpha = \alpha x^{\alpha - 1}. \] Note. In the final step of the calculation above, we used an index law. We first need to check that the index laws hold for our new definition of powers. (This is easy to do, since we have already established the index laws for \(\exp\) and the logarithm laws for \(\ln\).)
Exercise 21

We will give a proof assuming \(x>0\); the negative case is similar. Consider the integral

\[ \int_n^{n+x} \dfrac{1}{t} \; dt. \]

We can compute this exactly as

\begin{align*} \int_n^{n+x} \dfrac{1}{t} \; dt &= \bigl[ \ln t \bigr]_n^{n+x}\\ &= \ln(n+x) - \ln n\\ &= \ln \dfrac{n+x}{n}\\ &= \ln \Bigl( 1 + \dfrac{x}{n} \Bigr). \end{align*}

On the other hand, we can bound \(\dfrac{1}{t}\) on the interval \([n,n+x]\) by

\[ \dfrac{1}{n+x} \leq \dfrac{1}{t} \leq \dfrac{1}{n}. \]

Estimating the integral then gives

\[ \dfrac{x}{n+x} \leq \ln \Bigl( 1 + \dfrac{x}{n} \Bigr) \leq \dfrac{x}{n}. \]

Multiplying through by \(n\) yields

\[ \dfrac{xn}{n+x} \leq \ln \Bigl( 1 + \dfrac{x}{n} \Bigr)^n \leq x. \]

As \(n \to \infty\), \(\dfrac{xn}{n+x} \to x\), so we obtain \(\ln \Bigl( 1 + \dfrac{x}{n} \Bigr)^n \to x\), hence \(\Bigl(1 + \dfrac{x}{n}\Bigr)^n \to e^x\).