Content

A rigorous approach to logarithms and exponentials

What does an exponential mean anyway?

Throughout this module, we've assumed that functions like \(f(x) = 2^x\) are defined for all real numbers \(x\). But are they really?

There's no problem defining \(2^x\) when \(x\) is a positive integer; this just means repeated multiplication and is certainly well defined.

There's also no problem when \(x\) is a negative integer, using the index law

\[ 2^{-n} = \dfrac{1}{2^n}. \]

For example, \(2^{-3} = \dfrac{1}{8}\).

Nor is there a problem when \(x\) is a rational number. Using the index laws again,

\[ 2^\frac{a}{b} = (2^a)^{\frac{1}{b}} = \sqrt[b]{2^a}. \]

For example, \(2^\frac{3}{2} = \sqrt{2^3} = \sqrt{8} = 2\sqrt{2}\).

However, it's not so clear what to do when \(x\) is irrational. What does \(2^{\sqrt{2}}\) mean? So far in the module, this issue has been quietly suppressed.

One approach we might use is continuity. We could take a sequence of rational numbers \(r_1, r_2, r_3, \dotsc\) which approach \(\sqrt{2}\), and consider \(2^{r_1}, 2^{r_2}, 2^{r_3}, \dotsc\). If these numbers approach a limit, then we can call that limit \(2^{\sqrt{2}}\).

In any case, it's not a trivial matter to define exponential functions like \(2^x\) for irrational \(x\).

One way to avoid all of the difficulties is to develop the entire story a different way, starting with the logarithmic function. As discussed in the Motivation section, this approach may appear less natural but is more rigorous and abstract.

The natural logarithm, rigorously

We begin by defining the natural logarithm as an integral.

Definition

For any real number \(x>0\),

\[ \ln x = \int_1^x \dfrac{1}{t} \; dt. \]

This equation was exercise 11. It is now a definition.

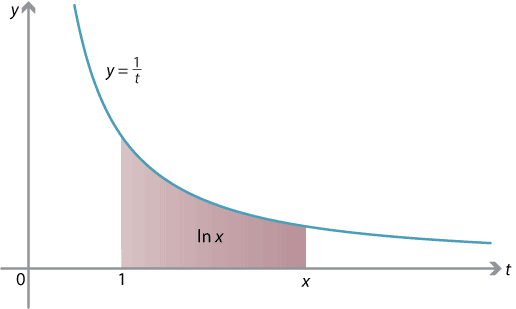
Definition of the natural logarithm as an integral.
Detailed description

As an aside, note the standard fact that the integral of \(t^n\) is

\[ \dfrac{1}{n+1} \, t^{n+1}. \]

This is true for any \(n \neq -1\). The integral above is of \(t^n\) when \(n = -1\), precisely the value of \(n\) for which this standard formula does not apply.

From this definition, we can see immediately that \(\ln 1 = 0\). We can also see, using the fundamental theorem of calculus, that the derivative of \(\ln x\) is \(\dfrac{1}{x}\). (We refer to the module Integration for the details). So the function \(\ln x\) is increasing, for all \(x > 0\), as its gradient \(\dfrac{1}{x}\) is positive. (This can also be seen from the diagram above, where \(\ln x\) is shown as a signed area.) It now follows that \(\ln x < 0\), for \(x \in (0,1)\), and \(\ln x > 0\), for \(x \in (1, \infty)\). It is clear that \(\ln x\) is a continuous function, and it's not too difficult to show that \(\ln x \to +\infty\) as \(x \to \infty\), and that \(\ln x \to -\infty\) as \(x \to 0\).

Our newly defined function \(\ln x\) and our previously defined function \(\log_e x\) both have the same derivative \(\dfrac{1}{x}\). Since \(\ln 1 = 0 = \log_e 1\), it follows that \(\ln x\) and \(\log_e x\) are in fact the same function — that is, if you manage to overcome all the difficulties with our previous definition of \(\log_e x\) and arrive at a well-defined function.

From the definition, it's not clear that the new function \(\ln x\) behaves like a logarithm at all. However, we will now show directly that this new function obeys the logarithm laws. We use a similar method to exercise 10.

Take a positive number \(y\), considered as a constant, and differentiate the two functions \(f(x) = \ln(xy)\) and \(g(x) = \ln x + \ln y\). We obtain

\[ f'(x) = \dfrac{y}{xy} = \dfrac{1}{x} \qquad \text{and} \qquad g'(x) = \dfrac{1}{x}, \] so \(f'(x) = g'(x)\), and therefore \(f(x), g(x)\) differ by a constant. As \(f(1) = \ln y = g(1)\), it follows that \(f(x) = g(x)\). This shows that \[ \ln(xy) = \ln x + \ln y, \] and so proves one of the logarithm laws.

Using a similar method, we can show that

\[ \ln \Bigl( \dfrac{x}{y} \Bigr) = \ln x - \ln y \] and \[ \ln \Bigl( \dfrac{1}{x} \Bigr) = - \ln x. \]

Next, consider the two functions \(f(x) = \ln(x^n)\) and \(g(x) = n \, \ln x\), where \(n\) is any rational number.³

Differentiating these functions gives

\[ f'(x) = \dfrac{1}{x^n} \cdot n x^{n-1} = \dfrac{n}{x} \qquad \text{and} \qquad g'(x) = \dfrac{n}{x}. \]

As \(f\) and \(g\) have the same derivative, they must differ by a constant. We further have \(f(1) = 0 = g(1)\), so \(f(x) = g(x)\) and we have proved the logarithm law

\[ \ln ( x^n ) = n \, \ln x. \]

As our new function \(\ln x\) obeys the familiar logarithm laws, we are justified in calling it a logarithm!

Exponentials, rigorously

Having established our new version of the natural logarithm function, we now turn to exponentials.

The function \(\ln x\) mapping \((0, \infty)\) to \(\mathbb{R}\) is a continuous function, strictly increasing from \(-\infty\) to \(+\infty\), and hence has an inverse function. This inverse function has domain \(\mathbb{R}\) and range \((0, \infty)\). We will, for the moment, call this inverse function \(\exp x\). So, by definition,

\[ \exp x = \ln^{-1}(x). \]

We then have

\begin{align*} \exp(\ln x) &= x \quad \text{for all positive \(x\),} \\ \ln( \exp x) &= x \quad \text{for all real \(x\).} \end{align*}

We define the number \(e\) to be \(\exp 1\). So \(\exp 1 = e\) and \(\ln e = 1\). It will turn out that \({\exp x = e^x}\); however this is not at all clear from the definition.

We can compute the derivative of \(\exp x\), since it is the inverse of \(\ln x\), and we know that the derivative of \(\ln x\) is \(\dfrac{1}{x}\). Let \(y = \exp x\). Then \(x = \ln y\) and we have

\[ \dfrac{dx}{dy} = \dfrac{1}{y}, \] so \[ \dfrac{d}{dx} \, \exp x = \dfrac{dy}{dx} = \dfrac{1}{\dfrac{dx}{dy}} = y = \exp x. \]

We can also show that \(\exp\) satisfies the index laws. For instance, we have

\begin{align*} \ln \bigl( \exp x \cdot \exp y \bigr) &= \ln (\exp x) + \ln (\exp y)\\ &= x+y\\ &= \ln \bigl(\exp (x+y)\bigr). \end{align*}

Here we just used a logarithm law and the fact that \(\ln\) and \(\exp\) are inverses. Since the function \(\ln\) is one-to-one and we have just shown that \(\ln \bigl( \exp x \cdot \exp y \bigr) = \ln \bigl(\exp (x+y)\bigr)\), we conclude the index law

\[ \exp x \cdot \exp y = \exp(x+y). \]

Using a similar method, we can show that \(\exp\) also obeys the index law

\[ \exp(x-y) = \dfrac{\exp x}{\exp y}. \]

For the remaining index law, take a rational number \(r\); we will show \(\exp(rx) = (\exp x)^r\). We observe

\begin{align*} \ln \bigl( (\exp x)^r \bigr) &= r \, \ln ( \exp x)\\ &= rx\\ &= \ln \bigl( \exp(rx) \bigr), \end{align*} where we just used a logarithm law and the fact that \(\ln\) and \(\exp\) are inverses. We have \(\ln \bigl( (\exp x)^r \bigr) = \ln \bigl( \exp(rx) \bigr)\), and cancelling \(\ln\)'s establishes the index law \[ (\exp x)^r = \exp(rx), \] for any rational number \(r\). Since \(\exp 1 = e\), we then have, for any rational number \(r\), \begin{align*} \exp r = \exp(r \cdot 1) = (\exp 1)^r = e^r. \end{align*}

We can now use this to define irrational powers. We declare for any real number \(x\), possibly irrational, that

\[ e^x = \exp x. \]

We can go further and use this idea to define any real power \(a^x\) of any positive number \(a\). When \(r\) is rational, we have from the index law above,

\[ \exp(r \, \ln a) = \bigl(\exp (\ln a ) \bigr)^r = a^r, \] and so for any real number \(x\) we can define \(a^x\) as follows.

Definition

For any real number \(x\) and any \(a>0\),

\[ a^x = \exp(x \, \ln a). \]

It's not difficult to show that \(a^x\) varies continuously with \(a\) and \(x\).

In this way, we have rigorously defined the functions \(\ln x\) and \(e^x\), found their derivatives, established the index and logarithm laws, and rigorously defined irrational powers.

Next page - Links forward - A series for e