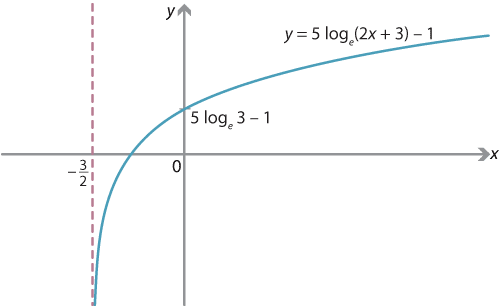Content

Graphing logarithmic functions

For any \(a>1\), the functions \(f(x) = a^x\) and \(g(x) = \log_a x\) are inverse functions, since

\[ f(g(x)) = a^{\log_a x} = x \] and \[ g(f(x)) = \log_a (a^x) = x. \]

The graphs of \(y=f(x)\) and \(y=g(x)\) are therefore obtained from each other by reflection in the line \(y=x\).

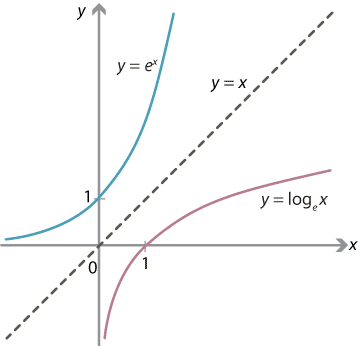
Graphs of y = log base e of x and y = 2 to the power of x showing that each one is the reflection of the other in the line y = x.
The symmetry between the graphs of \(y = e^x\) and \(y = \log_e x\).
Detailed description

The graph of the logarithmic function \(\log_a x\), for any \(a>1\), has the \(y\)-axis as a vertical asymptote, but has no critical points. Similarly, any other graph obtained from this graph by dilations, reflections in the axes and translations also has a vertical asymptote and no critical points.

Note. The graph of a logarithmic function does not have a horizontal asymptote. As \(x\) becomes large positive, the graph of \(y = \log_a x\) becomes very flat: the derivative

\[ \dfrac{dy}{dx} = \dfrac{1}{x \, \log_e a} \] approaches 0. Thus, \(\log_a x\) increases very slowly. However \(\log_a x\) still increases all the way to infinity: \[ \log_a x \to \infty \text{ \ as \ } x \to \infty. \]

One way to see this is to look at the symmetry in the graph above. The graph \(y=a^x\) is defined for all values of \(x\), but when \(x\) is large the corresponding value of \(y\) is very large. By symmetry, \(y = \log_a x\) takes all values of \(y\), but when \(y\) is large the corresponding value of \(x\) is very large.

Exercise 17

Prove directly that \(\log_a x\) can take an arbitrarily large value. Consider a large positive number \(N\). Does \(\log_a x\) ever take the value \(N\)?

Exercise 18

Show that there is a point on the graph of \(y=\log_e x\) such that, to go one unit upwards along the graph, you have to go a million units to the right.

That is, find \(x\) and \(y\) such that

\[ y = \log_e x \qquad \text{and} \qquad y + 1 = \log_e (x + 10^6). \]

Example

Draw the graph of \(y = 5 \,\log_e(2x+3)-1\).

Solution

The equation can be written as \(y = 5 f\bigl(2(x+\dfrac{3}{2})\bigr) - 1\), where \(f(x) = \log_e x\). Therefore, the graph is obtained from the graph of \(y = \log_e x\) by successively applying the following transformations:

dilation by a factor of \(\dfrac{1}{2}\) in the \(x\)-direction from the \(y\)-axis, which gives the graph of \(y = \log_e (2x)\)
dilation by a factor of 5 in the \(y\)-direction from the \(x\)-axis, which gives \(y = 5 \, \log_e (2x)\)
translation by \(\dfrac{3}{2}\) in the negative \(x\)-direction, giving \(y = 5 \, \log_e \bigl( 2(x + \dfrac{3}{2})\bigr) = 5 \, \log_e (2x+3)\)
translation by 1 in the negative \(y\)-direction, which gives \(y = 5 \, \log_e (2x+3) - 1\).

These transformations produce a vertical asymptote at \(x=-\dfrac{3}{2}\). There are no critical points.

Graph of y = 5 times log base e of 2x plus three and then one subtracted.
Detailed description

Exercise 19

Consider the graph \(y = \log_3 x\). Explain why the following two transformations of the graph have the same effect:

dilation in the \(x\)-direction from the \(y\)-axis with factor 9
translation by 2 units down (that is, in the negative \(y\)-direction).

Relate your answer to exercise 16.

Screencast of exercise 19

Next page - Content - A rigorous approach to logarithms and exponentials