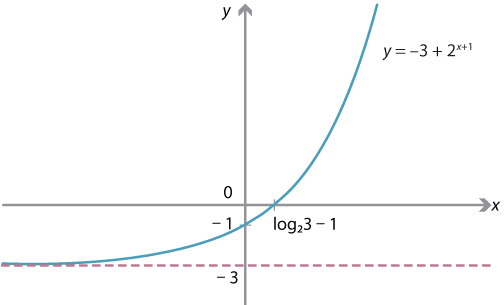Content

Graphing exponential functions

Having seen the general shape of the graphs \(y = a^x\), we can graph related functions, including those obtained by transformations such as dilations, reflections or translations.

Let us first revise these transformations; for more details, we refer to the module Functions II.

A dilation in the \(x\)-direction from the \(y\)-axis with factor \(k\) maps \[ (x,y) \mapsto (kx,y). \] The plane is stretched out horizontally from the \(y\)-axis by a factor of \(k\).
A dilation in the \(y\)-direction from the \(x\)-axis with factor \(k\) maps \[ (x,y) \mapsto (x,ky). \] The plane is stretched vertically from the \(x\)-axis by a factor of \(k\).
The reflection in the \(y\)-axis maps \[ (x,y) \mapsto (-x,y). \] The plane is reflected horizontally in the vertical axis: everything in the plane on one side of the \(y\)-axis goes to its mirror image on the other side of the \(y\)-axis.
The reflection in the \(x\)-axis maps \[ (x,y) \mapsto (x,-y). \] The plane is reflected vertically in the horizontal axis.
A translation in the \(x\)-direction by \(a\) units maps \[ (x,y) \mapsto (x+a, y). \] If \(a>0\), the translation is to the right, and if \(a<0\), the translation is to the left.
A translation in the \(y\)-direction by \(a\) units maps \[ (x,y) \mapsto (x, y+a). \] If \(a>0\), the translation is upwards, and if \(a<0\), the translation is downwards.

Note that, as the \(x\)-axis is an asymptote for the graph \(y=a^x\), any graph obtained by dilating, reflecting or translating such a graph will also have an asymptote.

Note also that, for any \(a>0\) with \(a \neq 1\), the function \(y=a^x\) has no critical points: the derivative \(\dfrac{dy}{dx} = \log_e a \cdot a^x\) is never 0. A graph obtained from \(y=a^x\) by dilations, reflections in the axes and translations also has no critical points.

Example

Sketch the graph of \(y = 2^{x+1}-3\).

Solution

This equation can be written as \(y=-3 + g(x+1)\) where \(g(x) = 2^x\). Hence the graph is obtained from \(y=2^x\) by successively performing the following transformations:

translation by 1 in the negative \(x\)-direction, which gives the graph of \(y=2^{x+1}\)
translation by 3 in the negative \(y\)-direction, which gives the graph of \(y=2^{x+1}-3\).

These transformations shift the asymptote to \(y=-3\).

Substituting \(x=0\) gives a \(y\)-intercept of \(-3+2= -1\). Substituting \(y=0\) gives \(2^{x+1} = 3\), so that \(x = \log_2 3 - 1\).

This is enough information to sketch the graph.

Graph of y = minus 3 plus2 to the power of x plus 1. It is the graph of y = 2 to the power of x. moved 1 unit to the left and 3 units down.
Detailed description

Note that, using the change of base rule, we can alternatively write the \(x\)-intercept of the graph as

\[ \log_2 3 - 1 = \dfrac{\log_e 3}{\log_e 2} - 1. \]

Exercise 14

Sketch the graph of \(y= 5 - 4 \cdot 3^{2x+1}\).

When \(0 < a < 1\), the graph \(y=f(x)\) of the function \(f(x)=a^x\) has a similar shape as for the case \(a>1\), but now \(f(x) \to 0\) as \(x \to \infty\) and \(f(x) \to \infty\) as \(x \to -\infty\).

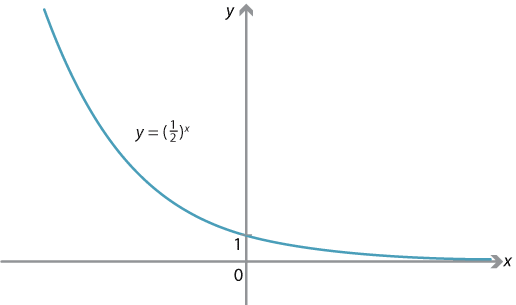
Graphs of y = one half to the power of x.
Graph of \(f(x) = \bigl( \dfrac{1}{2} \bigr)^x\).
Detailed description

Exercise 15

Explain why the graph of \(y = \bigl( \dfrac{1}{2} \bigr)^x\) is obtained from the graph of \(y=2^x\) by reflecting in the \(y\)-axis.
Hence sketch the graph of \(y = 3 - \bigl( \dfrac{1}{2} \bigr)^{x+1}\).

Exercise 16

Consider the graph \(y=3^x\). Explain why the following two transformations on the graph have the same effect:

dilation in the \(y\)-direction from the \(x\)-axis with factor 9
translation by 2 units to the left (that is, in the negative \(x\)-direction).

Next page - Content - Graphing logarithmic functions