Content

The natural logarithm

The logarithm to the base \(e\) is an important function. It is also known as the natural logarithm. It is defined for all \(x>0\):

\[ y = \log_e x \ \iff \ x = e^y. \]

The alternative notation \(\ln x\) (pronounced `ell-en' \(x\)) is often used instead of \(\log_e x\).

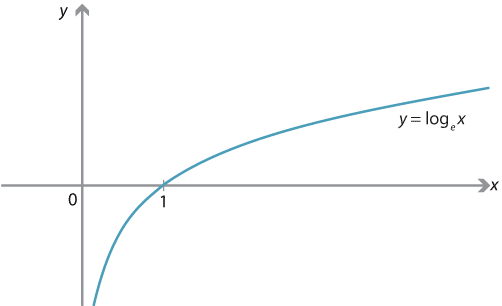
Graph of y = log base e of x.
Graph of \(y = \log_e x\) or, equivalently, \(x = e^y\).
Detailed description

Since we know how to differentiate the exponential, we can now also differentiate the natural logarithm. If \(y = \log_e x\), then \(x=e^y\), so

\[ \dfrac{dx}{dy} = e^y = x. \]

Now, by the chain rule, \(1 = \dfrac{dy}{dy} = \dfrac{dy}{dx} \dfrac{dx}{dy}\), and so

\[ \dfrac{dy}{dx} = \dfrac{1}{\dfrac{dx}{dy}} = \dfrac{1}{x}. \]

Therefore, we conclude that the derivative of \(f(x) = \log_e x\) is \(f'(x) = \dfrac{1}{x}\).

Exercise 3

Give an alternative proof that the derivative of \(\log_e x\) is \(\dfrac{1}{x}\), by differentiating both sides of the equation

\[ x = e^{\log_e x}. \]

Screencast of exercise 3 mp4 of screencast of exercise 3

Knowing the derivative of \(\log_e x\) allows us to differentiate many related functions.

Example

Find the derivative of \(f(x) = \log_e (2x+5)\).

Solution

The chain rule gives

\[ f'(x) = \dfrac{1}{2x+5} \cdot 2 = \dfrac{2}{2x+5}. \]

In general, for any real constants \(a\) and \(b\) with \(a \neq 0\), we can consider the function \({f(x) = \log_e(ax+b)}\). Its derivative is, again using the chain rule,

\[ f'(x) = \dfrac{a}{ax+b}. \]

A warning about domains. Any logarithm function \(\log_a x\), with base \(a>1\), is defined only for \(x>0\); its domain is \((0, \infty)\). Yet the function \(\dfrac{1}{x}\) is defined for all \(x \neq 0\), including all negative \(x\). Strictly speaking, the derivative of \(\log_e x\) is the function \(\dfrac{1}{x}\), restricted to the domain \((0, \infty)\).

In the previous example, \(\log_e(2x+5)\) is only defined when \(2x+5>0\), that is, \(x > - \dfrac{5}{2}\); so the functions \(f\) and \(f'\) both have domain \((-\dfrac{5}{2}, \infty)\).

Exercise 4

Consider the function \(f \colon (-\infty, 0) \to \mathbb{R}\) defined by \(f(x) = \log_e (-x)\). Show that \(f'(x) = \dfrac{1}{x}\), restricted to the domain \((-\infty, 0)\).

Using the preceding exercise, we can construct a function which is defined for all \(x \ne 0\), and whose derivative is always \(\dfrac{1}{x}\). We define \(f \colon \mathbb{R} \backslash \{0\} \to \mathbb{R}\) as

\[ f(x) = \log_e |x| = \begin{cases} \log_e x &\text{if \(x > 0\)}\\ \log_e (-x) &\text{if \(x < 0\).} \end{cases} \]

As both \(\log_e x\) and \(\log_e(-x)\) have derivative \(\dfrac{1}{x}\), we conclude that \(f'(x) = \dfrac{1}{x}\) for all \(x \neq 0\).

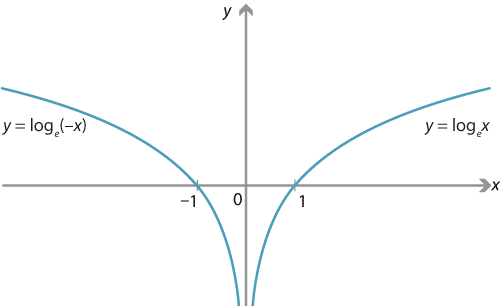
Graphs of y = log base e of x and y = log base e of minus x.
Graph of \(y = \log_e |x|\), which is the union of the graphs
\(y = \log_e x\), for \(x > 0\), and \(y = \log_e(-x)\), for \(x < 0\).
Detailed description

Exercise 5

What is the domain of the function \(f(x) = \log_2 (3-7x)\)?

The derivative of \(2^x\), revisited

We now obtain a simple answer to our original question.

Example

What is the derivative of \(f(x) = 2^x\)?

Solution

Since \(2 = e^{\log_e 2}\), we have \(f(x) = e^{\log_e 2 \cdot x}\). Using the chain rule, we obtain

\begin{align*} f'(x) &= \log_e 2 \cdot e^{\log_e 2 \cdot x}\\ &= \log_e 2 \cdot 2^x. \end{align*}

Previously we found that \(f'(x) \approx 0.693147 \cdot 2^x\). We now see that the constant is \(\log_e 2\).

Exercise 6

Find the derivatives of the following functions:

  1. \(f(x) = 2^{x^2}\)
  2. \(f(x) = 3^{4x^2 + 2x - 7}\).

Exercise 7

Use what we've done so far to explain why

\[ \lim_{h \to 0} \dfrac{2^h - 1}{h} = \log_e 2. \]

Next page - Content - Derivatives of general exponential functions