Content

How fast does an exponential function grow?

We will attempt to find the derivatives of exponential functions, beginning with \(2^x\). This is quite a long story, eventually leading us to introduce the number \(e\), the exponential function \(e^x\), and the natural logarithm. But we will then be able to differentiate functions of the form \(a^x\) in general.

The derivative of \(2^x\)

We begin by attempting to find the derivative of \(f(x) = 2^x\), which is graphed as follows.

Graph of \(f(x) = 2^x\).
Detailed description

Examining this graph, we can immediately say something about the derivative \(f'(x)\).

The graph of \(y = 2^x\) is always sloping upwards and convex down. For large negative \(x\), it is very flat but sloping upwards. As \(x\) increases, the graph slopes increasingly upwards; as \(x\) increases past 0, the gradient rapidly increases and the graph becomes close to vertical.

Therefore, we expect \(f'(x)\) to be:

• always positive
• increasing
• approaching 0 as \(x \to -\infty\)
• rapidly increasing for \(x\) positive
• approaching \(\infty\) as \(x \to \infty\).

In other words, we expect \(f'(x)\) to behave just like … an exponential function. (We will see eventually that \(f'(x) = \log_e 2 \cdot 2^x\).)

Let's first attempt to compute \(f'(0)\) from first principles:

\begin{align*} f'(0) &= \lim_{h \to 0} \dfrac{ f(h) - f(0) }{ h }\\ &= \lim_{h \to 0} \dfrac{ 2^h - 1 }{ h }. \end{align*}

This is not an easy limit to compute exactly, but we can approximate it by substituting values of \(h\).

Approximating \(f'(0)\) for the function \(f(x) = 2^x\)

\(h\)	\(\dfrac{2^h-1}{h}\) (to 6 decimal places)
0.001	0.693387
0.0001	0.693171
0.00001	0.693150
0.000001	0.693147
0.0000001	0.693147

From the table above, it appears that

\[ f'(0) = \lim_{h \to 0} \dfrac{2^h - 1}{h} \approx 0.693147. \]

Let us press on and attempt to compute \(f'(x)\) for \(x\) in general:

\begin{align*} f'(x) &= \lim_{h \to 0} \dfrac{ f(x+h)-f(x) }{ h } \\ &= \lim_{h \to 0} \dfrac{ 2^{x+h} - 2^x }{ h } \\ &= \lim_{h \to 0} \dfrac{ 2^x (2^h - 1) }{ h } \\ &= 2^x \cdot \lim_{h \to 0} \dfrac{2^h - 1}{ h }. \end{align*}

In the last step, we are able to take the \(2^x\) through the limit sign, since it is independent of \(h\). Note that the final limit is exactly the expression we found for \(f'(0)\). So we can now express the derivative as

\begin{align*} f'(x) &= f'(0) \cdot 2^x\\ &\approx 0.693147 \cdot 2^x. \end{align*}

We have found that the derivative of \(2^x\) is a constant times itself, confirming our initial expectations. (We will see later that this constant is \(\log_e 2\).)

The derivative of \(a^x\)

There is nothing special about the number 2 above. If we take any number \(a>1\) and consider \(f(x) = a^x\), the graph would have a similar shape to that of \(2^x\), and we could carry out similar computations for \(f'(0)\) and \(f'(x)\):

\begin{alignat*}{2} f'(0) &= \lim_{h \to 0} \dfrac{f(h) - f(0)}{h} &\qquad\qquad\qquad f'(x) &= \lim_{h \to 0} \dfrac{f(x+h)-f(x)}{h}\\ &= \lim_{h \to 0} \dfrac{a^h - 1}{h}, & &= \lim_{h \to 0} \dfrac{a^{x+h}-a^x}{h} \\ && &= a^x \cdot \lim_{h \to 0} \dfrac{a^h - 1}{h}. \end{alignat*}

We have found that, for any \(a>1\), the function \(f(x) = a^x\) has a derivative which is a constant multiple of itself:

\begin{align*} f'(x) &= a^x \cdot \lim_{h \to 0} \dfrac{a^h - 1}{h}\\ &= f'(0) \cdot a^x. \end{align*}

However, we need to better understand the limit involved. Clearly, if we can choose the value of \(a\) so that this limit is 1, then \(f'(x) = f(x)\) and so \(f\) is its own derivative.

The number \(e\)

Let's ponder further this limit for \(f'(0)\), the derivative at 0 of \(f(x) = a^x\):

\[ f'(0) = \lim_{h \to 0} \dfrac{a^h - 1}{h}. \]

We have already found that, when \(a=2\), the limit is approximately 0.693147. We can do the same calculations for other values of \(a\), and find the approximate limit. We obtain the following table.

Approximating \(f'(0)\) for functions \(f(x) = a^x\)

\(a\)	\(\displaystyle \lim_{h \to 0} \dfrac{a^h - 1}{h}\) (to 6 decimal places)
1	0
2	0.693147
3	1.098612
4	1.386294
5	1.609438

It appears that, when \(a\) increases, the limit for \(f'(0)\) also increases. This is not too difficult to prove.

Geometrically, this means that, as \(a\) increases, the graph of \(y=a^x\) becomes more sharply vertical, and the gradient of the graph at \(x=0\) increases.

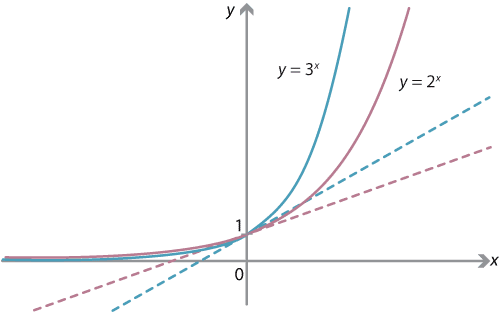
Graphs of \(y=2^x\) and \(y=3^x\) with tangents shown at \(x=0\).
Detailed description

When \(a=2\), we have a gradient at \(x=0\) of 0.69315. When \(a=3\), we have a gradient of 1.0986. So we expect that there is a single value of \(a\), between 2 and 3, for which the gradient at \(x=0\) is 1. It turns out that there is such a number, ² which we shall call \(e\). The number \(e\) is approximately 2.718281828.

Thus, the function \(f(x) = e^x\) has \(f'(0) = 1\) and, since \(f'(x) = f'(0) \cdot e^x\), we have \(f'(x) = e^x\). The function \(e^x\) is its own derivative. Equivalently, in Leibniz notation, \(y=e^x\) satisfies

\[ \dfrac{dy}{dx} = e^x \qquad \text{or, equivalently,} \qquad \dfrac{dy}{dx} = y. \]

The function \(f(x) = e^x\) is often called the exponential function, and sometimes written as \(\exp x\).

Note. This approach may appear to be a sleight of hand. We didn't really `prove' that the derivative of \(e^x\) is itself, we just defined \(e\) to make it true. But the key point is that there is a number \(e\) that makes the function \(e^x\) its own derivative. We have given an argument (although not a rigorous proof) as to why there is such a number.

Summary

• We considered the derivative of \(f(x) = 2^x\) and found that \begin{align*} f'(x) &= 2^x \cdot \lim_{h \to 0} \dfrac{2^h - 1}{h}\\ &\approx 0.693147 \cdot 2^x, \end{align*} so \(f'(x)\) is a constant multiple of \(f(x)\).
• We considered the derivative of the general function \(f(x) = a^x\), where \(a>1\), and found that \[ f'(x) = a^x \cdot \lim_{h \to 0} \dfrac{a^h - 1}{h}, \] so \(f'(x)\) is a constant multiple of \(f(x)\).
• We defined the number \(e\) so that the function \(f(x) = e^x\) is its own derivative, that is, \(f'(x) = f(x)\).

We will next introduce the natural logarithm. We will then be able to better express derivatives of exponential functions.

Next page - Content - The natural logarithm