History and applications

Some of the history of trigonometry was covered in earlier modules. The famous mathematician Euler, and his contemporaries Jacob and Johann Bernoulli, applied the ideas of calculus to the trigonometric functions producing remarkable results.

The mathematician Joseph Fourier, after whom Fourier series are named, applied the ideas of trigonometric series to solve physical problems — in particular, he looked at the distribution of heat in a metal bar.

One of the main modern applications of the trigonometric functions is to the analysis of signals and waves. Many different types of waves arise in the study of alternating currents and signals.

All of our modern telecommunications and electronic devices were only made possible by an understanding of the physics of electricity and the modern development of electrical engineering.

To give just a little insight into this, we are going to show how to build a 'sawtooth' wave using trigonometric functions.

The basic identities

\begin{align*} \cos A\,\cos B &= \dfrac{1}{2}\bigl(\cos(A-B)+\cos(A+B)\bigr) \\ \sin A\,\sin B &= \dfrac{1}{2}\bigl(\cos(A-B)-\cos(A+B)\bigr) \\ \sin A\,\cos B &= \dfrac{1}{2}\bigl(\sin(A-B)+\sin(A+B)\bigr) \end{align*}

can be established by expanding the right-hand sides. Using these identities, we can easily prove that, if \(m,n\) are positive integers, then

\[ \int_{-\pi}^\pi \sin mx\,\sin nx\, dx = \begin{cases} 0 &\text{if \(m\neq n\),}\\ \pi &\text{if \(m = n\).} \end{cases} \]

A similar formula holds for \(\cos mx\,\cos nx\). We can also show that

\[ \int_{-\pi}^\pi \cos mx\,\sin nx\, dx = 0, \]

for any integers \(m,n\).

We will attempt to construct the function \(y=x\), for \(x\in [-\pi,\pi]\), using an infinite sum of sine functions. We choose sine because the function \(y=x\) is odd, and so is the sine function. Thus we write:

\begin{align*} x &= b_1\sin x + b_2\sin 2x + b_3\sin 3x + \dotsb \\ &= \sum_{n=1}^\infty b_n\sin nx. \end{align*}

Multiplying both sides by \(\sin x\) and integrating from \(-\pi\) to \(\pi\), we have

\begin{align*} \int_{-\pi}^\pi x\,\sin x\, dx &= b_1\int_{-\pi}^\pi \sin x\,\sin x\, dx + b_2\int_{-\pi}^\pi \sin x\,\sin 2x\, dx + \dotsb \\ &= b_1\pi, \end{align*} so \[ b_1 = \dfrac{1}{\pi}\int_{-\pi}^\pi x\,\sin x\, dx. \]

Using the same idea, we can see that

\[ b_n = \dfrac{1}{\pi}\int_{-\pi}^\pi x\,\sin nx\, dx. \]

This integral can be found using a technique known as integration by parts, giving

\[ b_n= -\dfrac{2}{n}\cos n\pi. \]

The first few coefficients are

\[ b_1= 2, \quad b_2 = -1, \quad b_3 = \dfrac{2}{3}, \quad \dots \]

and so we have

\[ x = 2\Bigl(\sin x - \dfrac{1}{2}\sin 2x + \dfrac{1}{3}\sin 3x - \dfrac{1}{4}\sin 4x + \dfrac{1}{5}\sin 5x - \dfrac{1}{6}\sin 6x + \dotsb \Bigr), \]

at least for \(-\pi < x < \pi\).

It needs to be mentioned here that there are serious issues to be examined in regard to convergence, since we have an infinite series, but these issues are beyond the scope of this module.

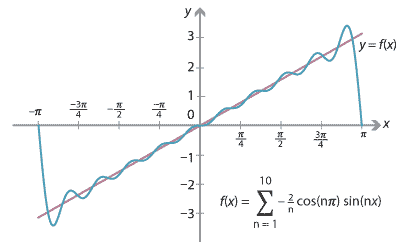
Graphically, we can chop the series off after a finite number of terms and plot. The following graph shows the sum of the first 10 terms.

Detailed description

Since the trigonometric functions are periodic, the series is converging to a periodic function, which takes copies of the line \(y=x\) and repeats them every \(2\pi\). This is an approximation of the sawtooth function shown at the start of this section. Note what happens near and at the jump discontinuity!

Next page - Answers to exercises