Links forward

The hyperbolic functions

In the 17th century, the mathematician Johann Bernoulli (and others) studied the curve produced by a hanging chain. It had been (incorrectly) thought by some that the curve was a parabola, but Bernoulli showed that its equation is very different. The curve is often referred to as a catenary (from the Latin word for chain) and, with appropriate choice of origin and scale, has the equation

\[ C(x)= \dfrac{e^x + e^{-x}}{2}. \]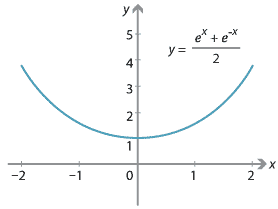

Detailed description
The catenary curve.

If we define

\[ S(x) = \dfrac{e^x - e^{-x}}{2}, \]

then it is easy to see that \(S'(x)= C(x)\) and \(C'(x)= S(x)\). Moreover, \(C(0)=1\) and \(S(0)=0\), and so these functions bear some similarity to the trigonometric functions \(\cos\) and \(\sin\) — although of course they are not periodic. (They do, however, have a complex period.) Hence, by analogy, \(C(x)\) is written as \(\cosh x\) (pronounced cosh of \(x\)) and \(S(x)\) is written as \(\sinh x\) (usually pronounced shine of \(x\)).

These function have other similarities to the trigonometric functions. For example, analogous to \(\cos^2 x + \sin ^2 x = 1\), we have

\[ \cosh^2 x - \sinh^2x = 1. \]

There are many other interesting analogues.

These functions are often called the hyperbolic functions (hence the 'h'), because this last identity enables us to parameterise half of the hyperbola

\[ \dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1 \]

by \(x=a\,\cosh t\), \(y=b\,\sinh t\).

The set of functions consisting of polynomials, rational functions, exponential and logarithmic functions, trigonometric functions and hyperbolic functions is often referred to as the set of elementary functions, since they are the most commonly occurring and well studied of all functions. Other functions which are not combinations of the above are sometimes referred to as special functions. An example of a special function is \(f(x)= \displaystyle \int_0^{x} e^{-t^2}\, dt\).

Next page - History and applications