Links forward

Inverse trigonometric functions

The sine and cosine functions are not one-to-one, and therefore they do not possess inverses. To overcome this problem, we have to restrict their domains, and find inverses for these functions with restricted domains. These issues are discussed in the module Functions I.

We will briefly discuss the sine function, and leave cosine as a directed exercise.

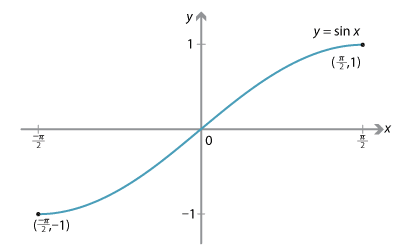
Note that \(\sin 0 = \sin \pi\), and so our chosen domain cannot include both 0 and \(\pi\). We can see that \(\sin\) is a one-to-one function on the interval \([-\dfrac{\pi}{2}, \dfrac{\pi}{2}]\), but not on any larger interval containing the origin.

We restrict the domain of \(y=\sin x\) to \([-\dfrac{\pi}{2}, \dfrac{\pi}{2}]\).

Graph of y = sin x between minus pi over 2 and pi over 2.
Detailed description

This restricted function, with domain \([-\dfrac{\pi}{2}, \dfrac{\pi}{2}]\) and range \([-1,1]\), is one-to-one. Hence, it has an inverse function denoted by \(f(x)=\sin^{-1} x\), which is read as inverse sine of \(x\). (This inverse function is also often denoted by \(\arcsin x\).)

It is important not to confuse \(\sin^{-1} x\) with \((\sin x)^{-1} = \dfrac{1}{\sin x}\); these are two completely different functions.

The graph of \(y=\sin^{-1} x\) is drawn as follows.

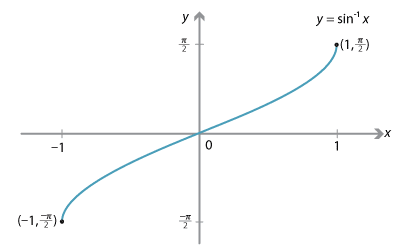
Graph of inverse sine drawn between minus one and one.

The domain of \(\sin^{-1}\) is \([-1,1]\) and its range is \([-\dfrac{\pi}{2},\dfrac{\pi}{2}]\). We can see from the graph that \(\sin^{-1}\) is an odd function, that is, \(\sin^{-1} (-x) = - \sin^{-1} x\). We can also see that it is an increasing function.

An obvious (and interesting) question to ask is 'What is its derivative?'

The derivative of inverse sine

We recall from the module Introduction to differential calculus that \(\dfrac{dy}{dx}\times \dfrac{dx}{dy} = 1\).

Let \(y=\sin^{-1} x\). Then \(x=\sin y\), and so

\begin{align*} \dfrac{dx}{dy} &= \cos y \\ &= \sqrt{1-\sin^2 y} \qquad\text{(since \(\cos y\geq 0\))} \\ &= \sqrt{1-x^2}. \end{align*}

Hence

\[ \dfrac{d}{dx} (\sin^{-1} x) = \dfrac{1}{\sqrt{1-x^2}}. \]

We observe from the graph of \(y=\sin^{-1}x\) that the gradient of the curve is positive. We can also see that the gradient approaches infinity as we approach \(x=1\) or \(x=-1\).

Using the chain rule, it is easy to show that

\[ \dfrac{d}{dx} \bigl(\sin^{-1} \dfrac{x}{a}\bigr) = \dfrac{1}{\sqrt{a^2-x^2}} \]

and so

\[ \int \dfrac{1}{\sqrt{a^2-x^2}}\, dx = \sin^{-1} \dfrac{x}{a} + C, \]

which gives us a new and important integral.

Exercise 13

  1. Restrict the domain of \(y=\cos x\) to the interval \([0,\pi]\). Draw a sketch to show that this restricted function is one-to-one, and write down the domain and range of its inverse \(y=\cos^{-1} x\).
  2. Explain graphically why \(\cos^{-1}(-x) = \pi - \cos^{-1}(x)\), and find \(\cos^{-1}(-\dfrac{1}{2})\).
  3. Show that the derivative of \(\cos^{-1} x\) is \(\dfrac{-1}{\sqrt{1-x^2}}\).
  4. Let \(f(x) = \sin^{-1} x + \cos^{-1} x\), for \(x\in [-1,1]\). Find the derivative of \(f\), and conclude that \(f\) is a constant function and find its value.

Next page - Links forward - The hyperbolic functions