Content
Simple harmonic motion
Simple harmonic motion (SHM) is a special case of motion in a straight line which occurs in several examples in nature. A particle \(P\) is said to be undergoing simple harmonic motion when it moves backwards and forwards about a fixed point (the centre of motion) so that its acceleration is directed back towards the centre of motion and proportional to its displacement from the centre.

Hence the displacement \(x\) of the particle \(P\) will satisfy the equation
\[ \dfrac{d^2x}{dt^2} = -n^2 x, \]where \(n\) is a positive constant.
This is an example of a second order differential equation. It can be shown that the general solution to this equation is \(x(t) = A\,\sin nt + B\,\cos nt\), where \(A\) and \(B\) are constants.
In the case where the particle starts at the origin, so \(x=0\) when \(t=0\), we have \(B=0\) and so the function \(x(t) = A\,\sin nt\) is a solution to the differential equation. We can easily check this:
\[ x(t) = A\,\sin nt \quad \implies \quad \dfrac{d^2x}{dt^2} = -n^2A\,\sin nt = -n^2 x. \]In the general case, since any trigonometric expression of the form \(A\,\sin \theta + B\,\cos \theta\) can written in the form \(C\,\sin(\theta + \alpha)\), we can write the general solution as
\[ x(t) = C\,\sin(nt + \alpha), \]where \(C\) and \(\alpha\) are constants. The constant \(\alpha\) is called the phase shift of the motion (and as we saw above can be taken as 0 if the particle begins at the origin). From our knowledge of the trigonometric functions, we see that the amplitude of the motion is \(C\) and the period is \(\dfrac{2\pi}{n}\).
We next derive a formula for the velocity of the particle, with the help of a very useful expression for acceleration: \(\dfrac{d^2x}{dt^2} = \dfrac{1}{2}\dfrac{d}{dx}(v^2)\). We write the differential equation as
\[ \dfrac{1}{2}\dfrac{d}{dx}(v^2) = -n^2 x \]and integrate with respect to \(x\) to obtain
\[ v^2 = K - n^2 x^2, \]where \(K\) is a constant. If the amplitude of the motion is \(C\), then when \(x=C\) the velocity is 0, and so \(K=n^2C^2\). Hence, we have
\[ v^2 = n^2(C^2- x^2). \]Example
A particle is moving in simple harmonic motion. Find a formula for the displacement \(x(t)\) of the particle (with \(x\) in metres and \(t\) in seconds) given that:
- the period of the motion is 16 seconds
- the particle passes through the centre of oscillation when \(t=2\)
- the particle has a velocity of \(2\pi\) m/s when \(t=4\).
What is the amplitude of the motion?
Solution
The general equation for simple harmonic motion is \(x = C\sin(nt+\alpha)\). Since the period is 16, we have \(\dfrac{2\pi}{n} = 16\), giving \(n = \dfrac{\pi}{8}\).
Also, since \(x = 0\) when \(t=2\), we have \(C \sin(2n+\alpha) = 0\). As \(C\neq 0\), we may take \(2n+\alpha = 0\), and so \(\alpha = -2n = -\dfrac{\pi}{4}\).
Finally, the velocity is given by
\[ v = \dfrac{dx}{dt} = Cn\,\cos(nt + \alpha) = \dfrac{C\pi}{8}\cos\Bigl(\dfrac{\pi}{8}t - \dfrac{\pi}{4}\Bigr). \]Now, \(v = 2\pi\) when \(t=4\), giving \(\dfrac{C\pi}{8} \cdot \dfrac{1}{\sqrt{2}} = 2\pi\), and so \(C=16\sqrt{2}\).
Thus the equation for displacement is
\[ x = 16\sqrt{2}\,\sin\Bigl(\dfrac{\pi}{8}t -\dfrac{\pi}{4}\Bigr) \]and the amplitude is \(16\sqrt{2}\).
Exercise 12
Find the speed of a particle moving in SHM when it is passing through the centre, if its period is \(\pi\sqrt{2}\) seconds and its amplitude is 2 metres.
Example
In a certain bay, there is a low tide of 6 metres at 1am and a high tide of 10 metres at 8am. Assuming that the tide motion is simple harmonic, find an expression for the height at time \(t\) after 1am, and find the first time after 1am when the tide is 9 metres.
Solution
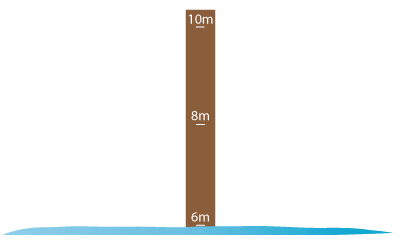
Let \(t\) be the time in hours since 1am, and let \(x\) be the height of the tide in metres at time \(t\). Since the centre of the motion is at 8 m and the amplitude is 2 m, we can express the height as \(x = 8 + 2\sin(nt +\alpha)\).
The period is 14 hours, so \(\dfrac{2\pi}{n}=14\), giving \(n=\dfrac{\pi}{7}\). Also, since \(x=6\) when \(t=0\), we may take \(\alpha = -\dfrac{\pi}{2}\). Hence the height of the tide is
\[ x = 8 + 2\sin\Bigl(\dfrac{\pi}{7}t - \dfrac{\pi}{2}\Bigr). \] (We can check that when \(t=7\), \(x=10\), as expected.)Now, when \(x=9\), we have \(\sin\Bigl(\dfrac{\pi}{7}t - \dfrac{\pi}{2}\Bigr) = \dfrac{1}{2}\). The smallest solution is \(t = \dfrac{14}{3}\), that is, 4 hours 40 minutes after 1am.
So the required time is 5:40am.
Hooke's law
An inextensible string is one which can bear a mass without altering its length. In practice, all strings are extensible, however the extension is usually very negligible. In the case of a string which is extensible, Hooke's law provides a simple relationship between the tension in the string and the extension it experiences. It states that the tension in an elastic string (or spring) is directly proportional to the extension of the string beyond its natural length.
Thus, if \(T\) is the tension in the spring, then \(T = kx\), where \(x\) is the extension and \(k\) is a positive constant, sometimes called the stiffness constant for the spring.
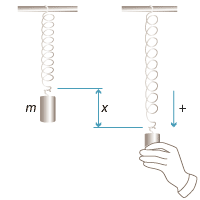
Suppose that we have a particle of mass \(m\) attached to the bottom of a vertical spring with stiffness constant \(k\). Since the system is stationary, the tension in the spring is given by \(mg\), where \(g\) is the acceleration due to gravity. By Hooke's law, the tension in the spring is also equal to \(ke\), where \(e\) is the extension of the natural length of the spring after the mass is added. We let the position of the particle at this stage be \(O\), and then further depress the mass by a displacement \(x\) from \(O\) and release it. The tension \(T\) in the spring is now \(T = k(e+x) = mg +kx\). The resultant downward force is then
\[ F = mg - T = -kx. \]This force produces an acceleration: by Newton's second law of motion, \(F = m \, \dfrac{d^2x}{dt^2}\). So we have
\[ \dfrac{d^2x}{dt^2} = -\dfrac{k}{m}x. \]This is the differential equation for simple harmonic motion with \(n^2 = \dfrac{k}{m}\). Hence, the period of the motion is given by \(\dfrac{2\pi}{n} = 2\pi\sqrt{\dfrac{m}{k}}\).
We can conclude that the larger the mass, the longer the period, and the stronger the spring (that is, the larger the stiffness constant), the shorter the period.