Content
Integrating trigonometric functions
Since integration is the reverse of differentiation, we have immediately that
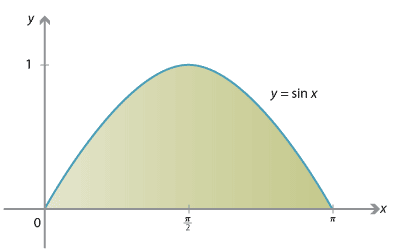
\[ \int \cos x\, dx = \sin x + C \qquad\text{and}\qquad \int \sin x\, dx = -\cos x + C. \]Thus, for example, we can find the area under the sine curve between \(x=0\) and \(x=\pi\), as shown on the following graph.
\[ \text{Area} = \int_0^\pi \sin x\, dx = \bigl[-\cos x\bigr]_0^\pi = 2. \]More generally, since
\[ \dfrac{d}{dx} \sin(ax+b) = a\,\cos(ax+b) \quad\text{and}\quad \dfrac{d}{dx} \cos(ax+b) = -a\,\sin(ax+b), \]we obtain, for \(a\neq 0\),
\[ \int \cos (ax+b)\, dx = \dfrac{1}{a}\sin (ax+b) + C \quad\text{and}\quad \int \sin (ax+b)\, dx = -\dfrac{1}{a}\cos (ax+b) + C. \]From \(\dfrac{d}{dx} (\tan x) = \sec^2x\), we obtain
\[ \int \sec^2 x\, dx = \tan x + C. \]Example
Find
- \(\displaystyle \int_0^{\frac{\pi}{2}} \bigl(1+\cos 2x\bigr)\, dx\)
- \(\displaystyle \int_0^{\frac{\pi}{6}} \bigl(\sin 3x+\sec^2 2x\bigr)\, dx\).
Solution
- \(\displaystyle \int_0^{\frac{\pi}{2}} \bigl(1+\cos 2x\bigr)\, dx = \Bigl[x+\dfrac{1}{2}\sin 2x\Bigr]_0^{\frac{\pi}{2}} = \dfrac{\pi}{2}\)
- \(\displaystyle \int_0^{\frac{\pi}{6}} \bigl(\sin 3x+\sec^2 2x\bigr)\, dx = \Bigl[-\dfrac{1}{3}\cos 3x + \dfrac{1}{2}\tan 2x \Bigr]_0^{\frac{\pi}{6}} = \dfrac{1}{3} + \dfrac{\sqrt{3}}{2}\).
Exercise 10
- Find \(\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{3}} (\sin 2x + \cos 3x)\, dx\).
- Differentiate \(x\,\sin x\), and hence find \(\displaystyle \int_0^\frac{\pi}{2} x\,\cos x\, dx\).
- Use the identity \(1+\tan^2x = \sec^2 x\) to find \(\displaystyle \int \tan^2 x\, dx\).
Special integrals
The two integrals
\[ \int \cos^2 \theta\, d\theta \qquad\text{and}\qquad \int \sin^2 \theta\, d\theta \]require some special attention. They are handled in similar ways.
To proceed, we make use of two trigonometric identities (a double-angle formula and the Pythagorean identity):
\[ \cos^2 \theta - \sin^2\theta = \cos 2\theta \qquad\text{and}\qquad \cos^2\theta + \sin^2\theta = 1. \]Adding these two identities, we have \(2\cos^2\theta = 1+ \cos2\theta\), and so we can replace \(\cos^2\theta\) in the integral with \(\dfrac{1}{2}(1+\cos 2\theta)\). Thus
\[ \int \cos^2 \theta\, d\theta = \int \dfrac{1}{2}(1+\cos 2\theta)\, d\theta = \dfrac{1}{2}\Bigl(\theta + \dfrac{1}{2}\sin 2\theta\Bigr) + C. \]Exercise 11
Find \(\displaystyle \int \sin^2 \theta\, d\theta\). (Follow the method used for \(\cos^2\theta\), but subtract the two identities rather than adding them.)