Content

An important limit

In order to apply calculus to the trigonometric functions, we will need to evaluate the fundamental limit

\[ \lim_{x\to 0} \dfrac{\sin x}{x}, \]

which arises when we apply the definition of the derivative of \(f(x) = \sin x\).

It must be stressed that, from here on in this module, we are measuring \(x\) in radians.

You can see that attempting to substitute \(x=0\) into \(\dfrac{\sin x}{x}\) is fruitless, since we obtain the indeterminate form 'zero over zero'. On the other hand, if we try substituting say \(x=0.1\) (in radians), then the calculator gives \(0.998\dots\), and if we try \(x=0.01\), we get \(0.99998\dots\).

We guess that, as \(x\) approaches 0, the value of \(\dfrac{\sin x}{x}\) approaches 1. We will now give a nice geometric proof of this fact.

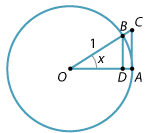
Consider a sector \(OAB\) of the unit circle containing an acute angle \(x\), as shown in the following diagram. Drop the perpendicular \(BD\) to \(OA\) and raise a perpendicular at \(A\) to meet \(OB\) produced at \(C\). Since \(OA = OB = 1\), we have \(BD = \sin x\) and \(AC = \tan x\).

Detailed description

The area of the sector \(OAB\) is \(\dfrac{1}{2} x\). The sector \(OAB\) clearly contains the triangle \(OAB\) and is contained inside the triangle \(OAC\). Hence, comparing their areas, we have

\begin{align*} \text{Area } \triangle OAB \leq \dfrac{1}{2} x \leq \text{Area } \triangle OAC \quad &\implies \quad \dfrac{1}{2}OA \cdot BD \leq \dfrac{1}{2} x \leq \dfrac{1}{2}OA \cdot AC \\ &\implies \quad \dfrac{1}{2}\sin x \leq \dfrac{1}{2} x \leq \dfrac{1}{2}\tan x \\ &\implies \quad \sin x \leq x \leq \tan x. \end{align*}

Now, since \(\tan x = \dfrac{\sin x}{\cos x}\) and since \(\sin x > 0\) for \(0 < x < \dfrac{\pi}{2}\), we can divide both inequalities by \(\sin x\) to obtain

\[ 1 \leq \dfrac{x}{\sin x} \leq \dfrac{1}{\cos x}. \]

Since \(\cos x\) approaches 1 as \(x\) approaches 0, we see that

\[ \dfrac{x}{\sin x} \to 1 \quad\text{as}\quad x\to 0. \]

Taking the reciprocal, it follows that

\[ \dfrac{\sin x}{x} \to 1 \quad\text{as}\quad x\to 0. \] (Here we have used the pinching theorem and the algebra of limits, as discussed in the module Limits and continuity.)

Thus we can write

\[ \lim_{x\to 0} \dfrac{\sin x}{x} = 1. \]

Note that this means that, if the angle \(x\) is small, then \(\sin x \approx x\). This fact is often used by physicists when analysing such things as a simple pendulum with small angle.

Other related limits can be found by manipulating this basic limit.

Next page - Content - Differentiating trigonometric functions