Content

Review of radian measure

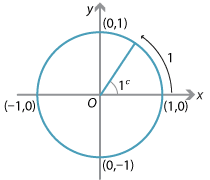
We saw in the module Trigonometric functions and circular measure that angles can be naturally defined using arc length.

We define 1 radian (written as \(1^c\)) to be the angle subtended in the unit circle by an arc length of one unit.

Detailed description

Since the circumference of the unit circle is \(2\pi\) and the angle in one revolution is \(360^\circ\), we can relate the two units by \(2\pi^c = 360^\circ\) or

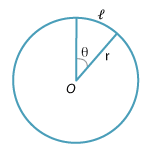
\[ \pi = 180^\circ. \] (As usual, we will drop the superscript \(c\) when it is clear that the angle under discussion is in radians.) Many commonly occurring angles can be expressed in radians as fractions of \(\pi\). For example, \(60^\circ = \dfrac{\pi}{3}\) and \(330^\circ = \dfrac{11\pi}{6}\).

We have also seen that the arc length \(\ell\) of a sector of a circle of radius \(r\), containing an angle \(\theta\) (in radians), is given by

\[ \ell = r\theta, \]

while the area \(A\) of the sector is given by

\[ A = \dfrac{1}{2}r^2\theta. \]

Next page - Content - An important limit