History and applications

The differential and integral calculus, as we have discussed it in these modules, using antiderivatives and the fundamental theorem of calculus, was developed in the 17th century by such mathematicians as Pierre de Fermat, James Gregory, Isaac Barrow, Isaac Newton and Gottfried Wilhelm Leibniz — but principally by Newton and Leibniz. However, some precursors to integration were known in ancient times.

Several ancient Greek philosophers and mathematicians considered the problem of calculating the area bounded by a curve. In the 5th and 4th centuries BCE, Antiphon and Eudoxus developed the idea of finding the area bounded by a curve by inscribing polygons in it, now known as the method of exhaustion. The idea is to inscribe infinitely many polygons within the curve, which do not overlap and which cover the entire area, so that the sum of the areas of polygons approaches the area bounded by the curve.

The method of exhaustion was perhaps taken furthest by Archimedes, who used it in the 3rd century BCE to perform calculations of areas and volumes bounded by circles, ellipses, spheres and cylinders. By calculating the area of the polygons inside and outside a circle, he was able to show that \(\frac{223}{71} < \pi < \frac{22}{7}\). He was also able to compute the area bounded by a chord in a parabola.

Though our notation is very different, Archimedes would have been able to calculate an integral like,

\[ \int_{-1}^1 (1 - x^2) \; dx. \]

It's interesting to compare our 'modern' (17th century CE) technique to Archimedes'. We would compute this area as

\[ \int_{-1}^1 (1-x^2) \; dx = \Bigg[ x - \frac{x^3}{3} \Bigg]_{-1}^1 = \Big( 1 - \frac{1}{3} \Big) - \Bigg( (-1) - \Big({-} \frac{1}{3} \Big) \Bigg) = \frac{2}{3} + \frac{2}{3} = \frac{4}{3}. \]

Although Archimedes did not have coordinate geometry, or even symbolic algebra, to work with, we can give a rough outline of his ideas in his work Quadrature of the parabola. (For further details, see the article Archimedes' quadrature of the parabola revisited listed in the References section.)

Detailed description of diagram

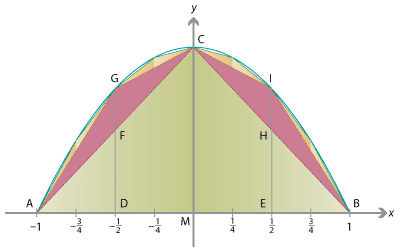
Using Archimedes' technique to find the area under a parabola.

We begin by inscribing a triangle in the parabola. Let \(A = (-1,0)\) and \(B = (1,0)\) be the intersection points of the chord (i.e., the \(x\)-axis) with the parabola, as shown in the diagram. Let \(M = (0,0)\) be the midpoint of \(AB\), and let \(C = (0,1)\). The area of \(\triangle ABC\) is 1, as it has width 2 and height 1.

We next inscribe two more triangles in the parabola, built on \(\triangle ABC\). Let \(D = (-\frac{1}{2},0)\) be the midpoint of \(AM\) and let \(E = (\frac{1}{2},0)\) be the midpoint of \(BM\). We draw a line from \(D\) parallel to the axis of the parabola (i.e., the \(y\)-axis), intersecting \(AC\) at \(F\) and intersecting the parabola at \(G = (-\frac{1}{2},\frac{3}{4})\). Similarly, we draw a line from \(E\) parallel to the parabola's axis, intersecting \(BC\) at \(H\) and intersecting the parabola at \(I = (\frac{1}{2}, \frac{3}{4})\). We consider the two triangles \(\triangle AGC\) and \(\triangle BIC\).

To compute the area of \(\triangle AGC\), we consider the segment \(FG\). The area is given by half the 'height' \(FG\) times the width of \(\triangle AGC\) in the \(x\)-direction. The width (in the \(x\)-direction) is half that of \(\triangle ABC\), i.e., 1. To compute \(FG\), note that \(\triangle ADF\) is similar to \(\triangle AMC\), so \(\frac{DF}{AD} = \frac{MC}{AM}\) and hence \(DF = AD \cdot \frac{MC}{AM} = \frac{1}{2}\). Thus \(FG = DG - DF = \frac{3}{4} - \frac{1}{2} = \frac{1}{4}\); the 'height' of \(\triangle AGC\) is a quarter that of \(\triangle ABC\). As \(\triangle AGC\) has half the width and a quarter the height of \(\triangle ABC\), it has an eighth the area. Similarly, we can compute that \(\triangle BIC\) has an eighth the area of \(\triangle ABC\).

As we proceed, we inscribe more and more triangles inside the parabola. In the next step we inscribe four triangles, after that we inscribe eight triangles. At the \(n\)th stage, we inscribe \(2^n\) triangles in the gaps between previous triangles. Archimedes was able to show that, at each stage, the triangles all have half the width and a quarter the height of the triangles from the previous stage, and hence an eighth the area.

The total area of all the triangles is given by a geometric series:

\[ 1 + \frac{2}{8} + \frac{2^2}{8^2} + \frac{2^3}{8^3} + \dotsb = 1 + \frac{1}{4} + \frac{1}{4^2} + \frac{1}{4^3} + \dotsb. \]

Using the formula

\[ 1 + r + r^2 + \dotsb = \frac{1}{1-r} \] for the limiting sum of a geometric series, the total area is \[ \frac{1}{1 - \frac{1}{4}} = \frac{4}{3}. \]

In this way, Archimedes succeeded in computing the area under the parabola.

Note. Archimedes actually did better than this. He used his technique to compute the area bounded by any chord in a parabola; the chord considered here is a special one (perpendicular to the axis of the parabola).

Next page - Appendix - A comparison of area estimates, and Simpson's rule