Links forward

Difficulties with antiderivatives

We saw in the modules on differentiation that many functions can be differentiated. Indeed, knowing how to differentiate elementary functions, and using the product, chain and quotient rules, we can find the derivative of most functions we come across.

So far in this module, we have been able to antidifferentiate every function we encountered. But as it turns out, there are some relatively simple functions for which the antiderivative has no simple formula. Although there are many techniques and tricks for finding antiderivatives, there are no rules as simple as the product, chain and quotient rules for differentiation.

For an interesting and important example, consider the function \(f \colon \mathbb{R}\) to \(\mathbb{R}\) defined by \(f(x) = e^{-x^2}\).

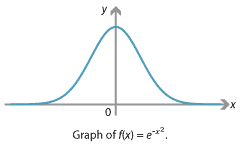
Detailed description of diagram

It is easy to differentiate \(f(x)\) using the chain rule: \(f'(x) = -2xe^{-x^2}\). However, the antiderivative of \(f(x)\) has no simple formula. Yet the integral of \(f(x)\) is very important, because it essentially describes the normal distribution, which is fundamental to probability and statistics.

It is possible to show that the integral of \(f(x)\), over the whole real line, is

\[ \int_{-\infty}^{+\infty} e^{-x^2} \; dx = \sqrt{\pi}. \]

This may seem to be a surprising result; it is not clear at all where the \(\pi\) came from.² Some clever techniques and higher mathematics, which are beyond our scope here, such as area integrals and polar coordinates, can be used to obtain this answer.

Next page - History and applications