Links forward

Arc length

How long is a piece of string? If the piece of string is given as a graph \(y = f(x)\) then its length can be calculated using integration.

As we have now seen many times, we consider the curve between \(x=a\) and \(x=b\) and split the \(x\)-interval into \(n\) subintervals \([x_0, x_1]\), \(\dots\), \([x_{n-1}, x_n]\) of length \(\Delta x\). Over each subinterval there is an arc segment that travels \(\Delta x\) to the right and \(\Delta y\) upwards, where \(\Delta y = f(x_j) - f(x_{j-1})\). Approximating the arc by straight line segments, the length of each line segment is \(\sqrt{(\Delta x)^2 + (\Delta y)^2}\). This gives an estimate for the length of the curve as

\[ \sum_{j=1}^n \sqrt{(\Delta x)^2 + (\Delta y)^2} = \sum_{j=1}^n \sqrt{1 + \Big( \frac{\Delta y}{\Delta x} \Big)^2} \; \Delta x. \]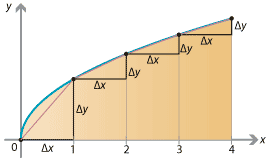

Detailed description of diagram

Taking the limit as \(n \to \infty\), the length of the curve is given by

\[ \int_a^b \sqrt{ 1 + \Big( \frac{dy}{dx} \Big)^2 } \; dx = \int_a^b \sqrt{ 1 + f'(x)^2 } \; dx. \]

Next page - Links forward - Difficulties with antiderivatives