Content
Area between two curves
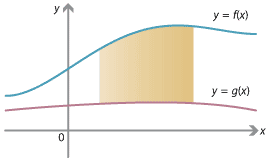
So far we have only found areas between the graph \(y=f(x)\) and the \(x\)-axis. In general we can find the area enclosed between two graphs \(y=f(x)\) and \(y=g(x)\). If \(f(x) > g(x)\), then the desired area is that which is below \(y=f(x)\) but above \(y=g(x)\), which is
\[ \int_a^b \big( f(x) - g(x) \big) \; dx. \]This formula works regardless of whether the graphs are above or below the \(x\)-axis, as long as the graph of \(f(x)\) is above the graph of \(g(x)\). (Can you see why?)
Detailed description of diagram
In general, two graphs \(y=f(x)\) and \(y=g(x)\) may cross. Sometimes \(f(x)\) may be larger and sometimes \(g(x)\) may be larger. In order to find the area enclosed by the curves, we can find where \(f(x)\) is larger, and where \(g(x)\) is larger, and then take the appropriate integrals of \(f(x) - g(x)\) or \(g(x) - f(x)\) respectively.
Example
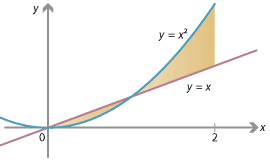
Find the area enclosed between the graphs \(y=x^2\) and \(y=x\), between \(x=0\) and \(x=2\).
Detailed description of diagram
Solution
Solving \(x^2 = x\), we see that the two graphs intersect at \((0,0)\) and \((1,1)\). In the interval \([0,1]\), we have \(x \geq x^2\), and in the interval \([1,2]\), we have \(x^2 \geq x\). Therefore the desired area is
\begin{align*} \int_0^1 ( x - x^2 ) \; dx \, + \int_1^2 ( x^2 - x ) \; dx &= \Bigg[ \frac{1}{2} x^2 - \frac{1}{3} x^3 \Bigg]_0^1 + \Bigg[ \frac{1}{3} x^3 - \frac{1}{2} x^2 \Bigg]_1^2 \\ &= \Bigg( \Big( \frac{1}{2} - \frac{1}{3} \Big) - \big( 0 \big) \Bigg) + \Bigg( \Big( \frac{8}{3} - 2 \Big) - \Big( \frac{1}{3} - \frac{1}{2} \Big) \Bigg) \\ &= \Big( \frac{1}{6} - 0 \Big) + \Bigg( \frac{2}{3} - \Big( {-} \frac{1}{6} \Big) \Bigg) \\ &= \frac{1}{6} + \frac{5}{6} = 1. \end{align*}Next page - Links forward - Integration and three dimensions
  |
This publication is funded by the Australian Government Department of Education, Employment and Workplace Relations |
Contributors Term of use |