Content

The area under a graph

Suppose you have a function \(f\colon \mathbb{R} \to \mathbb{R}\) and its graph \(y=f(x)\). You want to find the area under the graph. For now we'll assume that the graph \(y=f(x)\) is always above the \(x\)-axis, and we'll estimate the area between the graph \(y=f(x)\) and the \(x\)-axis. We set left and right endpoints and estimate the area between those endpoints.

Below is the graph of \(f(x)=x^2 + 1\). We'll try to find the area under the graph \(y=f(x)\) between \(x=0\) and \(x=5\), which is shaded.

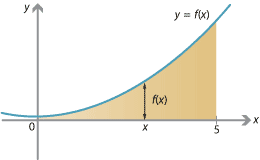
Graph of y = f(x) where f(x) = x squared + 1, part of parabola shown, area between graph and x axis between x = 0 and x =5 shaded. y coordinate at x is f(x).
Detailed description of diagram

As a first approximation, we can divide the interval \([0,5]\) into five subintervals of width 1, i.e., \([0,1]\), \([1,2]\), \(\dots\), \([4,5]\), and consider rectangles as shown on the following graph.

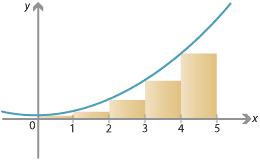
y = f(x) where f(x)= x squared + 1, parabola, 5 equal width rectangles between x = 0 and x = 5, with height of each rectangle determined by left value of x starting at x = 0.
Detailed description of diagram

As we can see, the total area of these rectangles is a rough approximation to the area we are looking for, but a clear underestimate. The total area of the rectangles is calculated in the following table.

Approximating the area under the graph with 5 rectangles
Interval	Width of rectangle	Height of rectangle	Area of rectangle
\([0,1]\)	1	\(f(0) = 0^2 + 1 = 1\)	1
\([1,2]\)	1	\(f(1) = 1^2 + 1 = 2\)	2
\([2,3]\)	1	\(f(2) = 2^2 + 1 = 5\)	5
\([3,4]\)	1	\(f(3) = 3^2 + 1 = 10\)	10
\([4,5]\)	1	\(f(4) = 4^2 + 1 = 17\)	17
		Total area	35

For a slightly better approximation, we can split the interval into 10 equal subintervals, each of length \(\frac{1}{2}\). Using the same idea, we have the rectangles shown on the following graph. We clearly have a better estimate, but still an underestimate.

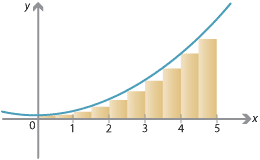
y = f(x) where f(x) = x squared + 1, parabola, 10 equal width rectangles between x = 0 and x = 5.
Detailed description of diagram

Approximating the area under the graph with 10 rectangles
Interval	Width of rectangle	Height of rectangle	Area of rectangle
\([0,\frac{1}{2}]\)	\(\frac{1}{2}\)	\(f(0) = 0 + 1 = 1\)	\(\frac{1}{2}\)
\([\frac{1}{2},1]\)	\(\frac{1}{2}\)	\(f(\frac{1}{2}) = \frac{1}{4} + 1 = \frac{5}{4}\)	\(\frac{5}{8}\)
\([1,\frac{3}{2}]\)	\(\frac{1}{2}\)	\(f(1) = 1 + 1 = 2\)	1
\([\frac{3}{2},2]\)	\(\frac{1}{2}\)	\(f(\frac{3}{2}) = \frac{9}{4} + 1 = \frac{13}{4}\)	\(\frac{13}{8}\)
\([2,\frac{5}{2}]\)	\(\frac{1}{2}\)	\(f(2) = 4 + 1 = 5\)	\(\frac{5}{2}\)
\([\frac{5}{2},3]\)	\(\frac{1}{2}\)	\(f(\frac{5}{2}) = \frac{25}{4} + 1 = \frac{29}{4}\)	\(\frac{29}{8}\)
\([3,\frac{7}{2}]\)	\(\frac{1}{2}\)	\(f(3) = 9 + 1 = 10\)	5
\([\frac{7}{2},4]\)	\(\frac{1}{2}\)	\(f(\frac{7}{2}) = \frac{49}{4} + 1 = \frac{53}{4}\)	\(\frac{53}{8}\)
\([4,\frac{9}{2}]\)	\(\frac{1}{2}\)	\(f(4) = 16 + 1 = 17\)	\(\frac{17}{2}\)
\([\frac{9}{2},5]\)	\(\frac{1}{2}\)	\(f(\frac{9}{2}) = \frac{81}{4} + 1 = \frac{85}{4}\)	\(\frac{85}{8}\)
		Total area	\(\frac{325}{8} = 40.625\)

Splitting \([0,5]\) into more subintervals of smaller width, we can perform the same calculation and estimate the area. With more rectangles, the calculations become more tedious, but some results are given in the following table.

Approximating the area under the graph with more rectangles
Number of intervals	Width of each interval	Total area of rectangles
5	1	35
10	0.5	40.625
50	0.1	45.425
100	0.05	46.04375
1 000	0.005	46.6041875
10 000	0.0005	46.66041875
100 000	0.00005	46.66604166875
1 000 000	0.000005	46.6666041666875

With more and more thinner and thinner rectangles, the areas appear to be converging towards a limit. It turns out, as we will see, that the limit is \(46 \frac{2}{3}\).

Screencast of interactive 4 , Interactive 4

The area under a curve is defined to be this limit. Although we have an intuitive notion of what area is, for a mathematically rigorous definition we need to use integration.

Next page - Content - Estimates of area